Question

The cost of 5 apples and 3 oranges is Rs.35 and the cost of 2 apples and 4 oranges is Rs.28. Formulate the problem algebraically and solve it graphically.

Answer 1

Hint: We have to find the cost of apples and oranges from the given information, thus we have to take the costs of the apples and oranges as two variables and then write the given information algebraically.

Complete step-by-step answer:

As we have to find the cost of each apple and orange, we can take the cost of an apple to be the variable x and the cost of an orange to be the variable y.
Now, it is given that the cost of 5 apples and three oranges is Rs.35. In our notation, this corresponds to the equation
$5x+3y=35................(1.1)$
Also, it is given that the cost of 2 apples and 4 oranges is Rs.28. In our notation, this corresponds to the equation
$2x+4y=28................(1.2)$
Thus, equations(1.1) and (1.2) represent the algebraic formulation of the problem.
To solve the problem graphically, we notice that equations (1.1) and (1.2) correspond to two straight lines which contain the points satisfying the first and second conditions given by equations (1.1) and (1.2) respectively. Therefore, we should plot the lines corresponding to the equations (1.1) and (1.2) on the same graph. The point of their intersection would be the point which satisfies both equations and thus should be the answer to the given question.

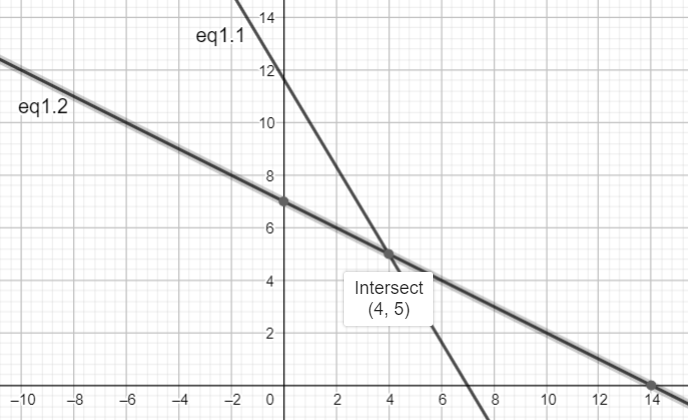
From the above plot where equation 1.1 and 1.2 are plotted, we find that the lines intersect at the point x=4, y=5.
Thus, we obtain the answer to the question as
Cost of each apple= x = Rs.4
Cost of each orange= y = Rs.5

Note: In this question, as the equations represented lines, the lines intersected at only one point. In higher degree equations, the curves may intersect at more than one point. In that case, each intersection point would be a valid answer to the question.