Question

The correct Biot-Savart law in vector form is?
\[
  A.{\text{ }}d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{I\left( {d\vec l \times \vec r} \right)}}{{{r^2}}} \\
  B.{\text{ }}d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{I\left( {d\vec l \times \vec r} \right)}}{{{r^3}}} \\
  C.{\text{ }}d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Id\vec l}}{{{r^2}}} \\
  D.{\text{ }}d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Id\vec l}}{{{r^3}}} \\
 \]

Answer 1

- Hint: In order to deal with this question first we will understand the Biot-Savart law, then we will proceed further by considering the Biot-Savart law formula and by changing it in vector form we will get the answer.

Formula used- $d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Idl\sin \theta }}{{{r^2}}}\hat r,\hat r = \dfrac{{\vec r}}{r}$

Complete step-by-step answer:
Biot-Savart’s law: The law of Biot-Savart is an equation that gives the magnetic field generated as a result of an individual carrying a fragment. This section is taken as the individual entity known as the vector quantity.
Figure:

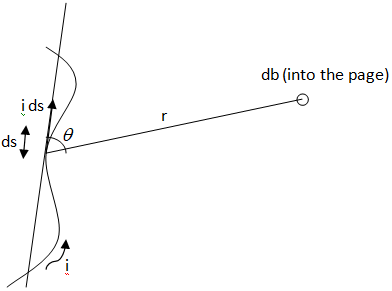
Biot-Savart’s law formula: Consider a current carrying wire $I$ in a specific direction as shown in the above figure. Take a small element of the wire of length $dl$ . The direction of this element is along that of the current so that it forms a vector $Id\vec l$ .
One can apply the Law of Biot-Savart to know the magnetic field produced at a point due to this small element. Let the position vector of the point in question drawn from the current element be r and the angle between the two be $\theta $. Then,
$d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Idl\sin \theta }}{{{r^2}}}\hat r$
Where
${\mu _0}$ is the permeability of free space and is equal to $4\pi \times {10^{ - 7}}Tm{A^{ - 1}}$ .
So the Biot Savart's Law formula is
Now we know:
$\hat r = \dfrac{{\vec r}}{r}$
Using this and the cross product we obtain from two vectors;
$
  \because d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Idl\sin \theta }}{{{r^2}}}\hat r \\
   \Rightarrow d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Id\vec l\sin \theta }}{{{r^2}}}\dfrac{{\vec r}}{r} \\
   \Rightarrow d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{I\left( {d\vec l.\vec r\sin \theta } \right)}}{{{r^2} \times r}} \\
   \Rightarrow d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{I\left( {d\vec l \times \vec r} \right)}}{{{r^3}}}{\text{ }}\left[ {\because \vec a \times \vec b = ab\sin \theta } \right] \\
 $
Hence, the correct Biot-Savart law in vector form is $d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{I\left( {d\vec l \times \vec r} \right)}}{{{r^3}}}$
Hence the correct answer is option B.

Note: The Biot – Savart Law is an equation that describes the magnetic field produced by a constant electric current. It relates magnetic fields to electric current magnitude, direction, length, and proximity. Also at the atomic or molecular stage we can use the Biot – Savart rule to measure magnetic responses. It is also used for measuring the velocity caused by the vortex lines in aerodynamic theory.