Question

The coordinates of three points O, A, B are $\left( {0,0} \right)$, $\left( {0,4} \right)$and$\left( {6,0} \right)$ respectively, a point P moves so that area of triangle POA is always twice the area of triangle POB. Find the equation for both parts of locus of P.
A) $\left( {x - 3y} \right)\left( {x - 3y} \right) = 0$
B) $\left( {x + 3y} \right)\left( {x + 3y} \right) = 0$
C) $\left( {x - 3y} \right)\left( {x + 3y} \right) = 0$
D) None of these

Answer 1

Hint:
To solve this question let point P lies on $\left( {x,y} \right)$. Draw the triangle on the graph according to the question and then find the area of both the triangle i.e. \[\vartriangle POA\] and \[\vartriangle POB\] by the formula given below:
$ \Rightarrow A = \dfrac{1}{2} \times b \times h$, ………..(1)
Where A is the area of the triangle, b be the base of the triangle and h be the height of the triangle.
Now, equate the area of both the triangles as given in the question i.e.
$ \Rightarrow {A_1} = 2{A_2}$, where ${A_1}$ is the area of \[\vartriangle POA\] and ${A_2}$ is the area of \[\vartriangle POB\].

Complete step by step solution:
Let us see what is given to us? We are given with the coordinates of three points i.e. $O\left( {0,0} \right)$, $A\left( {0,4} \right)$and $B\left( {6,0} \right)$.
We have to find the equation of point P to both parts of the locus such that the area of \[\vartriangle POA\] is equal to twice the area of \[\vartriangle POB\].
$ \Rightarrow {A_1} = 2{A_2}$, ………..(2)
where ${A_1}$ is the area of \[\vartriangle POA\]and ${A_2}$ is the area of \[\vartriangle POB\].
First of let us assume Point P coordinates as $\left( {x,y} \right)$. After that draw the triangles as given in the question on graph. The graph is given as follow:

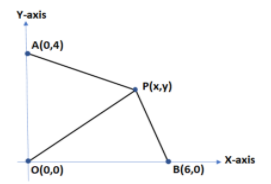
To find ${A_1}$, we draw a line perpendicular from point M at AO to meet at point P and To find ${A_2}$, we draw a line perpendicular from point N at BO to meet at point P as given in figure below:

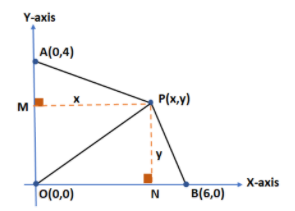
To find area of \[\vartriangle POA\], find AO and PM by distance formula i.e.
\[ \Rightarrow AO = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]
By putting the values of their respective co-ordinates, we get,
\[ \Rightarrow AO = \sqrt {{{\left( {0 - 0} \right)}^2} + {{\left( {4 - 0} \right)}^2}} \]
By opening the bracket and solving it, we get,
\[ \Rightarrow AO = 4\] ………..(3)
Similarly,
\[ \Rightarrow PM = \sqrt {{{\left( {x - 0} \right)}^2} + {{\left( {y - y} \right)}^2}} \]
By opening the bracket and solving it, we get,
\[ \Rightarrow PM = x\] …………(4)
Hence, area of \[\vartriangle POA\]can be calculated from formula (1) as
$ \Rightarrow {A_1} = \dfrac{1}{2} \times AO \times PM$
Putting the value of AO and PM from (3) and (4), we get,
$ \Rightarrow {A_1} = \dfrac{1}{2} \times 4 \times x$
By solving it we get,
$ \Rightarrow {A_1} = 2x$ ……..(5)
To find area of \[\vartriangle POB\], find BO and PN by distance formula i.e.
\[ \Rightarrow BO = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]
By putting the values of their respective co-ordinates, we get,
\[ \Rightarrow BO = \sqrt {{{\left( {6 - 0} \right)}^2} + {{\left( {0 - 0} \right)}^2}} \]
By opening the bracket and solving it, we get,
\[ \Rightarrow BO = 6\] ………..(6)
Similarly,
\[ \Rightarrow PN = \sqrt {{{\left( {x - x} \right)}^2} + {{\left( {y - 0} \right)}^2}} \]
By opening the bracket and solving it, we get,
\[ \Rightarrow PN = y\] …………(7)
Hence, area of \[\vartriangle POA\]can be calculated from formula (1) as
$ \Rightarrow {A_2} = \dfrac{1}{2} \times BO \times PN$
Putting the value of BO and PN from (6) and (7), we get,
$ \Rightarrow {A_2} = \dfrac{1}{2} \times 6 \times y$
$ \Rightarrow {A_2} = 3y$ …………(8)
By putting the value of area from (5) and (8) in equation (2), we get,
\[ \Rightarrow 2x = 2\left( {3y} \right)\]
By opening the bracket, we get,
\[ \Rightarrow 2x = \pm 6y\]
By cancelling 6 with 2, we get,
$$ \Rightarrow x = \pm 3y$$
$$ \Rightarrow \left( {x + 3y} \right)\left( {x - 3y} \right)$$

Hence, option C is the required answer.

Note:
It is noted that we have taken two values i.e. one is positive and other is negative while comparing the areas. As it is not given that point P lies in the first quadrant so we consider both the conditions that P can be on the first quadrant or on the fourth quadrant.
If we are given the quadrant of P then we have to take respective signs.
Some students forget to draw the line perpendicularly and take the other side as height which is the wrong method.