Question

The co-ordinates of one end point of a diameter of a circle are (4, -1) and co-ordinates of the centre of circle are (1, -3). Then coordinates of the other end of the diameter are
(A) (2,5)
(B) (-2, -5)
(C) (3,2)
(D) (-3, -2)

Answer 1

Hint: We start solving this problem by assuming the given endpoint as A and centre as O and the other endpoint as B and radius as r. Then we find the ratio of OB and AB. Then we use the formula for the point dividing two points in the ratio m:n externally, that is $\left( \dfrac{m{{x}_{2}}-n{{x}_{1}}}{m-n},\dfrac{m{{y}_{2}}-n{{y}_{1}}}{m-n} \right)$ and find the coordinates of B.

Complete step-by-step answer:
We are given that one end point of a circle is (4, -1). We are also given that coordinates of the centre of the circle are (1, -3).
Let us assume that the radius of the circle as r and given endpoint as A and centre as O. Let the other endpoint that we need to find be B.

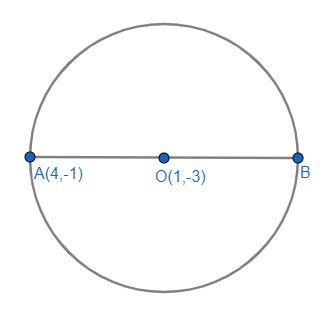
As OA and OB are the radius of the circle, we have OA=OB=r.
AB is the diameter of the circle. So, we have AB=2r.
Let us consider the ratio of OB and AB
$\dfrac{OB}{AB}=\dfrac{r}{2r}=\dfrac{1}{2}$
It means that B divides O and A in the ratio 1:2 externally.
Now let us consider the formula for the coordinates of the point dividing two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ in the m:n externally is
$\left( \dfrac{m{{x}_{2}}-n{{x}_{1}}}{m-n},\dfrac{m{{y}_{2}}-n{{y}_{1}}}{m-n} \right)$
Using this formula, we can find the coordinates of B as,
$\begin{align}
  & \Rightarrow \left( \dfrac{1\left( 4 \right)-2\left( 1 \right)}{1-2},\dfrac{1\left( -1 \right)-2\left( -3 \right)}{1-2} \right) \\
 & \Rightarrow \left( \dfrac{4-2}{-1},\dfrac{-1+6}{-1} \right) \\
 & \Rightarrow \left( \dfrac{2}{-1},\dfrac{5}{-1} \right) \\
 & \Rightarrow \left( -2,-5 \right) \\
\end{align}$
So, coordinates of the centre of the circle is (-2, -5).

So, the correct answer is “Option B”.

Note: We can also solve this question in another method. As we have above that OA=OB=r,
it means that O divides A and B in the equal ratio, that is O is the midpoint of A and B.
Now, let us consider the formula for the co-ordinates of the midpoint of two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is
$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
Let us assume that the coordinates of B as (a, b). Then using the above formula, we have
$\begin{align}
  & \Rightarrow \left( \dfrac{4+a}{2},\dfrac{-1+b}{2} \right)=\left( 1,-3 \right) \\
 & \Rightarrow \left( 4+a,-1+b \right)=\left( 2,-6 \right) \\
 & \Rightarrow \left( a,b \right)=\left( 2-4,-6+1 \right) \\
 & \Rightarrow \left( a,b \right)=\left( -2,-5 \right) \\
\end{align}$
Hence, we get the coordinates of B as (-2, -5).
Hence the answer is Option B.