Question

The condition that the chord of the ellipse \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\] whose midpoint \[\left( {x{}_1,{y_1}} \right)\]subtends a right angle at the center is
A.\[\dfrac{{x_1^2}}{{{a^4}}} + \dfrac{{y_1^2}}{{{b^4}}} = {\left( {\dfrac{{{x_1}}}{{{a^2}}} + \dfrac{{{y_1}}}{{{b^2}}}} \right)^2}\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)\]
B.\[\dfrac{{x_1^2}}{{{a^4}}} + \dfrac{{y_1^2}}{{{b^4}}} = {\left( {\dfrac{{x_1^2}}{{{a^2}}} + \dfrac{{y_1^2}}{{{b^2}}}} \right)^2}\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)\]
C.\[\dfrac{{x_1^2}}{{{a^4}}} + \dfrac{{y_1^2}}{{{b^4}}} = {\left( {\dfrac{{x_1^2}}{{{a^2}}} - \dfrac{{y_1^2}}{{{b^2}}}} \right)^2}\left( {\dfrac{1}{{{a^2}}} - \dfrac{1}{{{b^2}}}} \right)\]
D.\[\dfrac{{x_1^2}}{{{a^4}}} - \dfrac{{y_1^2}}{{{b^4}}} = {\left( {\dfrac{{{x_1}}}{{{a^2}}} - \dfrac{{{y_1}}}{{{b^2}}}} \right)^2}\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)\]

Answer 1

Hint: An ellipse is a plane curve surrounding two focal points, such that for all points on the curve the sum of the two distances to the focal points is constant. It is a conic section formed by the intersection of a right circular cone by a plane that cuts the axis and the surface of the cone.

Complete step-by-step answer:
Given the equation of ellipse \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\]

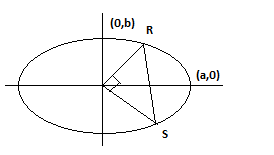
Here RS is the chord,
We know the equation of chord in terms of its midpoint \[\left( {x{}_1,{y_1}} \right)\]is given by the equation
\[\dfrac{{x{x_1}}}{{{a^2}}} + \dfrac{{y{y_1}}}{{{b^2}}} = \dfrac{{x_1^2}}{{{a^2}}} + \dfrac{{y_1^2}}{{{b^2}}}\]
Now homogenizing equation of ellipse w.r.t equation of chord
\[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = {\left( {\dfrac{{\dfrac{{x{x_1}}}{{{a^2}}} + \dfrac{{y{y_1}}}{{{b^2}}}}}{{\dfrac{{x_1^2}}{{{a^2}}} + \dfrac{{y_1^2}}{{{b^2}}}}}} \right)^2}\]
Since it represents a perpendicular pair of straight lines then the coefficient of \[{x^2}\]=-coefficient of \[{y^2}\]
Therefore, \[\dfrac{{x_1^2}}{{{a^4}}} + \dfrac{{y_1^2}}{{{b^4}}} = {\left( {\dfrac{{x_1^2}}{{{a^2}}} + \dfrac{{y_1^2}}{{{b^2}}}} \right)^2}\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)\]
So, the correct answer is “Option B”.

Note: Students should be aware about the properties of the ellipse to solve these types of questions. Moreover, the coordinates of the points which lie on the ellipse will always satisfy the equation of the ellipse.