Question

The collar A is free to slide along the smooth shaft B mounted in the frame. The plane of the frame is vertical. Determine the horizontal acceleration $a$ of the frame necessary to maintain the collar in a fixed position on the shaft.$\left( {g = 9.8\,m/{s^2}} \right)$

A.$5.66\,m/{s^2}$
B.$6.66\,m/{s^2}$
C.$2.83\,m/{s^2}$
D.$1.33\,m/{s^2}$

Answer 1

Hint-When a frame is accelerated then it is said to be a non-inertial frame. In such a frame there will be a pseudo force. The value of this pseudo force is $m\,a$ in the given question.
There are three forces acting on the collar, they are pseudo force, force due to gravity and normal reaction force. The collar will remain at a fixed position if these forces balance each other.
The pseudo force should be balanced by the sine component of normal force which is directly acting opposite to it. Similarly, the force due to gravity must be balanced by the cosine component of normal reaction force.
First equate the pseudo force and the component of normal force, then, we get
$ma = N\sin {30^ \circ }$
Then, equate force due to gravity and component of normal force
$mg = N\cos {30^ \circ }$
On comparing these two equations we can find the value of $a$.

Step by step solution:
From the figure we can see that it is a non-inertial frame. An inertial frame is a frame in which there is no acceleration. When acceleration is present then the frame is said to be a non-inertial frame.
The horizontal acceleration is given as $a$
So, there will be a pseudo force acting on the collar. The value of this force will be $m\,a$
For the collar to remain in fixed position all the forces acting on it should be in equilibrium.
Let us redraw the figure showing all the forces acting on the collar. The forces are pseudo force, force due to gravity and normal reaction force.

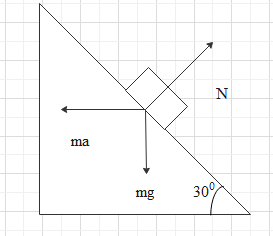
Now the collar will remain at a fixed position if these forces balance each other.
The pseudo force should be balanced by the sine component of normal force which is directly acting opposite to it. Similarly, the force due to gravity must be balanced by the cosine component of normal reaction force.
Let us use this to find the value of acceleration.
Here, the pseudo force =$m\,a$
Component of normal force acting opposite to it =$N\cos \theta $
From the figure we know, $\theta = {30^ \circ }$
Let us first equate the pseudo force and the component of normal force, then, we get
$ma = N\sin {30^ \circ }$
$ma = \dfrac{N}{2}$.......................(1)
Now let us equate force due to gravity and component of normal force
$mg = N\cos {30^ \circ }$
$mg = \dfrac{{\sqrt 3 }}{2}N$..................(2)
Divide equation (1) by (2). Then we get,
$\dfrac{{ma}}{{mg}} = \dfrac{{\dfrac{N}{2}}}{{\dfrac{{\sqrt 3 N}}{2}}} = \dfrac{1}{{\sqrt 3 }}$
$\therefore a = \dfrac{g}{{\sqrt 3 }}$
The value of acceleration due to gravity is given as $g = 9.8\,m/{s^2}$
Let us substitute this value. Then, we get
$a = \dfrac{{9.8}}{{\sqrt 3 }} = 5.66\,m/{s^2}$
This is the horizontal acceleration required .

So, the answer is option A

Note:Remember that any frame under acceleration will be a non-inertial frame. In such a frame there will be presence of pseudo force. Pseudo force is a fictitious force acting on the mass in the non-inertial frame. So, while trying to balance the forces to find acceleration when the collar will stay stationary, we should also include this pseudo force. The value of this pseudo force is $m\,a$ in the given question. Where, $m$ is the mass and $a$ is the acceleration.