Question

The coefficient of static friction between the two blocks shown in figure isμand the table is smooth. What maximum horizontal force F can be applied to the block of mass M so that the blocks move together?

Answer 1

Hint: It is one of the available renewable energy sources. It can operate with a very high capacitor factor and so can operate in base load mode. It is the process that produces electricity by using the temperature between deep cold ocean water and warm tropical surface water.As we all know that when a sudden force is applied on a vehicle in one direction, the person inside the vehicle experiences a backward force in the opposite direction then tends to move the body. That force is known as a pseudo force.

Complete answer:
Refer to the below figure for the free body diagram.

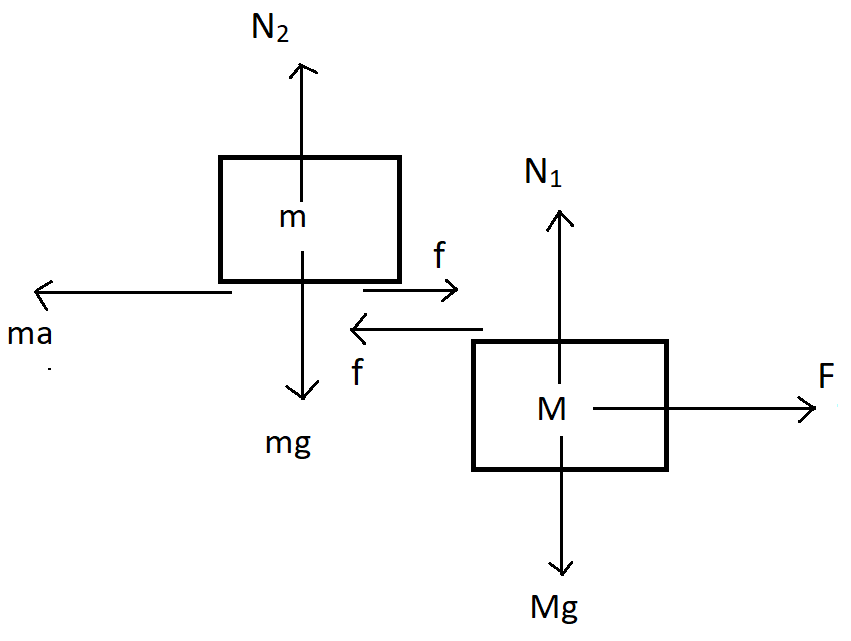
So here we can see that when the force F is applied on the bigger block of mass M, the bigger block wants to move forward. The smaller block of mass m which is placed above the bigger block tries to move backward due to pseudo force $ma$, which is balanced by the static frictional force $f$ .
Hence therefore we can say that for block of mass m, if we balance the horizontal force then,
$f = ma$
${N_2} = mg$
Here g is the acceleration due to gravity and ${N_2}$ is the normal reaction.
As we know that if the static frictional force f is applied on the block of mass m, then the same frictional force f is applied by the mass m on the block of mass Mbut in the opposite direction.
As the mass M has gained an acceleration, so we can apply Newton's third law of motion in it.
$ \Rightarrow F - f = {F_{net}}$ …… (I)
Here, ${F_{net}}$ is the net force on the block of mass M, which is responsible for its motion.
But as both blocks have to move together then the acceleration of both the blocks have to be the same.
Therefore, we can say that,
${F_{net}} = Ma$ …… (II)
So, we put the value of equation (II) in equation (I), therefore we can say that,
$ \Rightarrow F - f = Ma$ …… (III)
Also we know that for the block of mass m, the static frictional force is,
$
  f = \mu {N_2} \\
  \therefore f = \mu mg \\
 $
And we also know that
$f = ma$ …… (IV)
Now we will substitute $f = \mu mg$ in equation (IV) to find the value of a.
$
  \mu mg = ma \\
   \Rightarrow a = \mu g \\
 $
Now, we will substitute $f = ma$ in equation (III) to find the value of F.
$ \Rightarrow F - ma = Ma$
$ \Rightarrow F = (M + m)a$ ….. (V)
Now we will substitute $a = \mu g$ in equation (V) to find the value of force F.
$\therefore F = (M + m)\mu g$

$\therefore$ The maximum horizontal forced F can be applied to the block of mass M so that the blocks move together is $F = (M + m)\mu g$

Note:
Suppose in the given case, if there is friction is not enough and the relative sliding takes place among the blocks then, in that case, the acceleration of both the blocks is different and the smaller block may slide down from the bigger block.