Question

The circle $ {{x}^{2}}+{{y}^{2}}+2x-4y+1=0 $ touches
A. X-axis
B. Y-axis
C. both axes
D. none of these

Answer 1

Hint: We first try to form the given circle in its general form of $ {{\left( x-\alpha \right)}^{2}}+{{\left( y-\beta \right)}^{2}}={{r}^{2}} $ to find the centre and the radius. We put the values for the x and y coordinates as 0 and get only 1 value for the other coordinate. For any other number of solutions, the circle doesn’t touch the axis. We also confirm it by using the formula.

Complete step by step answer:
It’s given that the equation of the circle is $ {{x}^{2}}+{{y}^{2}}+2x-4y+1=0 $ . We transform it in its general form of $ {{\left( x-\alpha \right)}^{2}}+{{\left( y-\beta \right)}^{2}}={{r}^{2}} $ and get $ {{\left( x+1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}={{2}^{2}} $ . O is the centre.
Equating with the general equation of circle $ {{\left( x-\alpha \right)}^{2}}+{{\left( y-\beta \right)}^{2}}={{r}^{2}} $ , we get the centre as $ O\equiv \left( -1,2 \right) $ and the radius as 2 units.

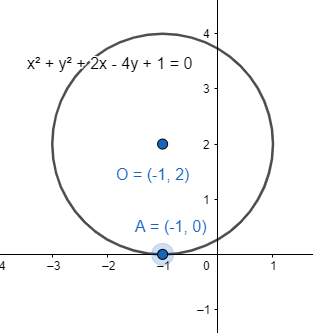
We get that if it touches any axes then we can put the for the x and y coordinates as 0 and get only 1 value for the other coordinate. If we get no solutions or two solutions, then we can say it doesn’t touch the axes.
We put $ x=0 $ and get $ {{\left( y-2 \right)}^{2}}=3 $ which gives $ y=2\pm \sqrt{3} $ . The circle doesn’t touch the Y-axis. It intersects at two points.
Now if we put $ y=0 $ and get $ {{\left( x+1 \right)}^{2}}=0 $ which gives $ x=-1 $ . The circle touches the X-axis at point $ A\equiv \left( -1,0 \right) $ .
The correct option is A.

Note:
 We also can use the formula that for a general equation of circle $ {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 $ , if the equation $ {{g}^{2}}=c $ satisfies then it touches the X-axis and if the equation $ {{f}^{2}}=c $ satisfies then it touches the Y-axis. For touching both axes the required equation would be $ {{f}^{2}}={{g}^{2}}=c $ .