Question

The centroid divides each median of a triangle in the ratio……………………………

Answer 1

Hint: First draw the medians of a triangle, medians are the line segments, which joins the midpoint of a side to its opposite vertex. All three medians intersect at common point. Then extend a median at some different point and form a parallelogram, then use in a parallelogram the diagonals bisect each other to find out the required ratio.

Complete step by step answer:
Let us, draw a triangle with all three medians first,

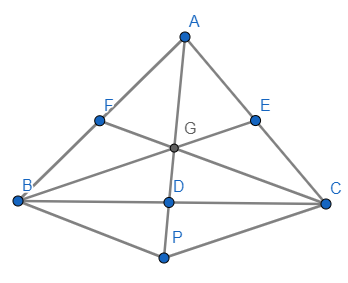
Here AD, BE, CF are the medians and G is the centroid of the $\Delta ABC$ .
This means
$\begin{align}
  & AC=2AE=2EC \\
 & AB=2AF=2BF \\
 & BC=2BD=2DC \\
\end{align}$
Let's produce AD to P such that AG = GP and join BP and CP.
Now in $\Delta ABC$ we have \[GF||BP\] and F and G are the mid points on AB and AP.
Therefore, from the midpoint theorem we can write, $GC\parallel BP$
Similarly, in $\Delta ACP$ we have $GE\parallel CP$ and E and G are the mid points on AC and AP.
Therefore, from the midpoint theorem we can write, $BG\parallel CP$.
This means BGCP is a parallelogram because, $GC\parallel BP$ and $BG\parallel CP$.
Now as we know in a parallelogram the diagonals bisect each other, therefore,
$GD=DP$
But, $AG=GP$
This means,
$\begin{align}
  & AG=GD+DP \\
 & \Rightarrow AG=2GD \\
 & \Rightarrow \dfrac{AG}{GD}=\dfrac{2}{1} \\
\end{align}$
So, that means the median AD is divided in a 2:1 ratio by the centroid G. A similar case procedure can be repeated on all the medians and the ratio will be the same i.e., 2:1 .

Hence, the centroid divides each median of a triangle in the ratio 2:1 .

Note: The caution must be taken when making the lines parallel to each other and applying the mid-point theorem. There should be a valid reason for each substitution.
Another approach is by using concurrency of triangles.