Question

The centers of two circles ${C_1}$ and ${C_2}$ each of unit radius are at distance 6 units from each other. Let P be the midpoint of the line segment joining the centers of ${C_1}$ and ${C_2}$ and C be circle touching circles ${C_1}$ and ${C_2}$ externally. If a common tangent to ${C_1}$ and C passing through P is also a common tangent to ${C_2}$ and C, then the radius of the circle C is,

Answer 1

Hint: In this particular question first draw the pictorial representation of the above problem it will give us a clear picture of what we have to find out, and use the concept that in a right triangle tan is the ratio of perpendicular to the base, so use these concepts to reach the solution of the question.

Complete step-by-step solution:

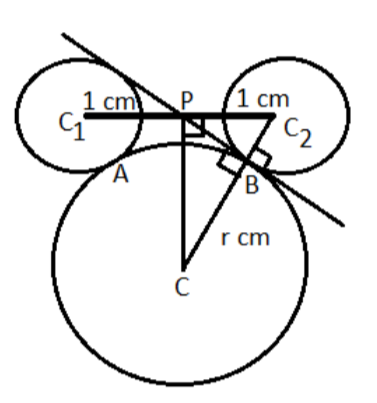
The pictorial representation of the problem is shown above, ${C_1}$ and ${C_2}$ have 1 cm radius each and the distance between centers is 6 cm.
P is the midpoint line joining the centers of ${C_1}$ and ${C_2}$.
Therefore, $ \Rightarrow {C_1}P = {C_2}P = \dfrac{{{C_1}{C_2}}}{2} = \dfrac{6}{2} = 3$ cm.
Now C be the circle which touches both the circles as shown above, and by symmetry, the line joining the center of the circle and point P is perpendicular on the line joining ${C_1}$ and ${C_2}$, as shown in the figure.
The common tangent to ${C_1}$ and C passing through P is also a common tangent to ${C_2}$ and C as shown in the above figure.
And ${C_2}B$ = 1cm (radius of the circle ${C_2}$)
Let the radius of the circle C is r.
Now as we know that the radius of the circle with the tangent of the circle always makes 90 degrees, as shown in the above figure.
So, in the right triangle, ${C_2}PB$ apply Pythagoras theorem we have,
$ \Rightarrow {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2} = {\left( {{\text{hypotenuse}}} \right)^2}$
$ \Rightarrow {\left( {{\text{PB}}} \right)^2} + {\left( {{\text{B}}{{\text{C}}_2}} \right)^2} = {\left( {{\text{P}}{{\text{C}}_2}} \right)^2}$
$ \Rightarrow {\left( {{\text{PB}}} \right)^2} + {\left( 1 \right)^2} = {\left( 3 \right)^2}$
$ \Rightarrow {\left( {{\text{PB}}} \right)^2} = 9 - 1 = 8$
$ \Rightarrow {\text{PB}} = \sqrt 8 = 2\sqrt 2 $ cm.
Now let angle $BP{C_2} = x$
So in triangle $BP{C_2}$ we have,
$ \Rightarrow \tan x = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}} = \dfrac{{B{C_2}}}{{PB}}$
Now substitute the values we have,
$ \Rightarrow \tan x = \dfrac{1}{{2\sqrt 2 }}$................ (1)
Now if, $\angle BP{C_2} = x$
Therefore, $\angle BPC = {90^o} - \angle BP{C_2} = {90^o} - x$
And $\angle PBC = {90^o}$
So in triangle PBC we have,
$ \Rightarrow \angle PBC + \angle BPC + \angle BCP = {180^o}$
Now substitute the values we have,
$ \Rightarrow {90^o} + {90^o} - x + \angle BCP = {180^o}$
$ \Rightarrow \angle BCP = x$
So in triangle BPC we have,
$ \Rightarrow \tan x = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}} = \dfrac{{PB}}{{BC}}$
Now substitute the values we have,
$ \Rightarrow \dfrac{1}{{2\sqrt 2 }} = \dfrac{{2\sqrt 2 }}{r}$
$ \Rightarrow r = 2\sqrt 2 \left( {2\sqrt 2 } \right) = 8$ Cm.
So the radius of the circle C is 8 cm.
So this is the required answer.

Note: Whenever we face such types of questions the key concept we have to remember is that the radius of the circle with the tangent of the same circle always makes 90 degrees so consider the right triangles as above considered first apply Pythagoras theorem in a small right triangle and find out the length of PB as above, then by geometry prove that $\angle BP{C_2} = \angle BCP$, then use the property of tan in both the right triangles as above we will get the required radius of the circle C.