
The center of a square ABCD is at $z = 0$ . A is ${z_1}$ . Then the centroid of triangle ABC is
A. ${z_1}(\cos \pi \pm i\sin \pi )$
B. $\dfrac{{{z_1}}}{3}(\cos \pi \pm i\sin \pi )$
C. ${z_1}\left( {\cos \dfrac{\pi }{2} \pm i\sin \dfrac{\pi }{2}} \right)$
D. $\dfrac{{{z_1}}}{3}\left( {\cos \dfrac{\pi }{2} \pm i\sin \dfrac{\pi }{2}} \right)$
Answer
573k+ views
Hint: First we’ll find the coordinate of vertices of triangle ABC using the rotation formula of the complex number, after that, we’ll use the property that centroid whose formula is given by the average of the coordinates of the vertices of a triangle. Using this we’ll find the coordinate for centroid but the order of square ABCD can be clockwise or anticlockwise so we’ll consider both the cases.
Complete step by step answer:
Given data: Center of square ABCD is at $z = 0$ and A is ${z_1}$.
Now we know that the center is $z = 0$, we can say that z is the intersection point and midpoint of both the diagonals as diagonal of a square bisect each other.

From the figure, we can say that Z is the midpoint of side AC as AC is the diagonal of square ABCD
Therefore we can say that C will be$ - {z_1}$ as C is equidistant from the origin as A and is exactly opposite to A.
We know that in complex number when any point let ${z_k}$ is rotated through an angle $\theta $ with-respect-to origin in the anticlockwise direction then the new point will be${z_k}{e^{i\theta }}$
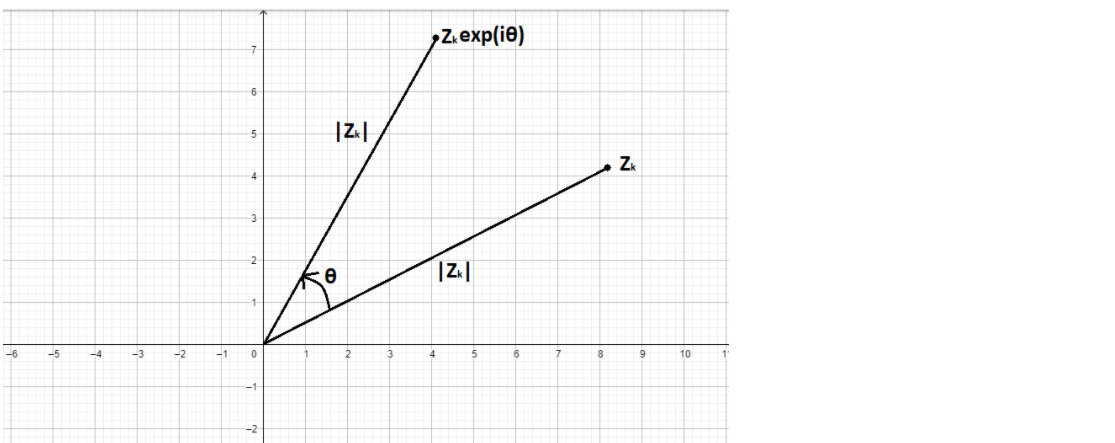
Similarly, we can say that B will be ${z_1}{e^{ - i\dfrac{\pi }{2}}}$since the origin is the center of square ABCD and the diagonals are perpendicular to each other.
Now we know that coordinate of a centroid is given by the average of the coordinates of the vertices of the triangle.
Therefore in triangle ABC coordinate of centroid will be $\dfrac{{{z_1} + {z_1}{e^{ - i\dfrac{\pi }{2}}} - {z_1}}}{3}$
$ = \dfrac{{{z_1}}}{3}{e^{ - i\dfrac{\pi }{2}}}$
Now, from the above case, we can say that centroid of the triangle ABC is $\dfrac{{{z_1}}}{3}{e^{ - i\dfrac{\pi }{2}}}$
In the above case, the vertices ABCD are in clock wise, but if the ABCD make an anti-clockwise sequence i.e.
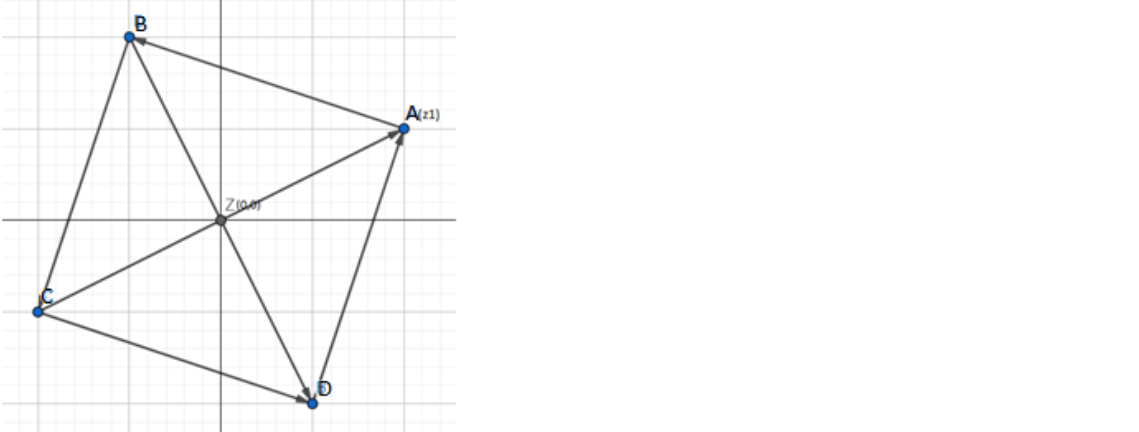
Now in this case B will be ${z_1}{e^{i\dfrac{\pi }{2}}}$ resulting the centroid to be $\dfrac{{{z_1}}}{3}{e^{i\dfrac{\pi }{2}}}$.
From the above results, we can say that centroid of the triangle ABC is $\dfrac{{{z_1}}}{3}{e^{ \pm i\dfrac{\pi }{2}}}$
Using ${e^{i\theta }} = \cos \theta + i\sin \theta $
$ \Rightarrow \dfrac{{{z_1}}}{3}{e^{ \pm i\dfrac{\pi }{2}}} = \dfrac{{{z_1}}}{3}\left( {\cos \left( { \pm \dfrac{\pi }{2}} \right) + i\sin \left( { \pm \dfrac{\pi }{2}} \right)} \right)$
Using $\cos \theta = \cos \left( { - \theta } \right)$and$\sin \left( { - \theta } \right) = - \sin \theta $
$ \Rightarrow \dfrac{{{z_1}}}{3}{e^{ \pm i\dfrac{\pi }{2}}} = \dfrac{{{z_1}}}{3}\left( {\cos \dfrac{\pi }{2} \pm i\sin \dfrac{\pi }{2}} \right)$
Option(D) is correct.
Note: In the above solution we stated that when a point let ${z_k}$ is rotated through an angle $\theta $ with-respect-to origin in the anticlockwise direction then the new point will be${z_k}{e^{i\theta }}$, we apply this formula only when the point is measured with-respect-to origin and both the resultant complex number and the original number is equidistant from the origin and if not then we use the general formula.
Complete step by step answer:
Given data: Center of square ABCD is at $z = 0$ and A is ${z_1}$.
Now we know that the center is $z = 0$, we can say that z is the intersection point and midpoint of both the diagonals as diagonal of a square bisect each other.

From the figure, we can say that Z is the midpoint of side AC as AC is the diagonal of square ABCD
Therefore we can say that C will be$ - {z_1}$ as C is equidistant from the origin as A and is exactly opposite to A.
We know that in complex number when any point let ${z_k}$ is rotated through an angle $\theta $ with-respect-to origin in the anticlockwise direction then the new point will be${z_k}{e^{i\theta }}$
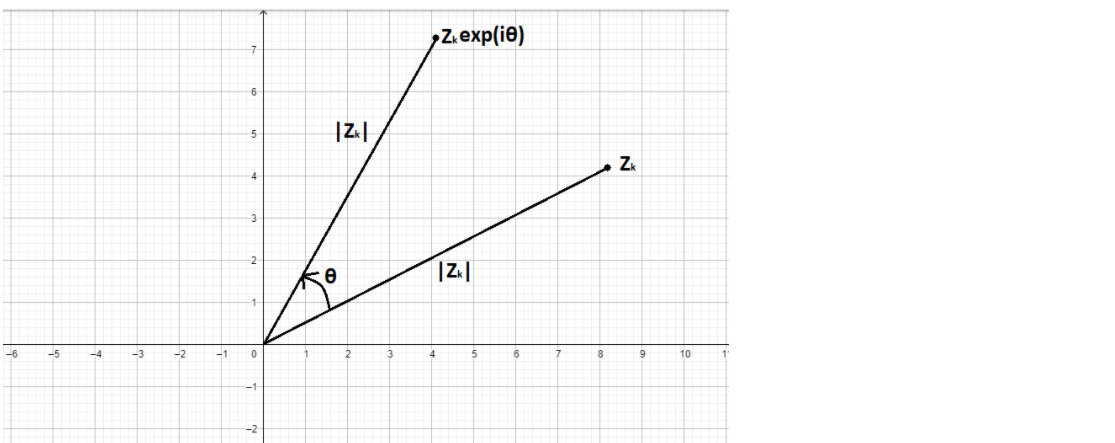
Similarly, we can say that B will be ${z_1}{e^{ - i\dfrac{\pi }{2}}}$since the origin is the center of square ABCD and the diagonals are perpendicular to each other.
Now we know that coordinate of a centroid is given by the average of the coordinates of the vertices of the triangle.
Therefore in triangle ABC coordinate of centroid will be $\dfrac{{{z_1} + {z_1}{e^{ - i\dfrac{\pi }{2}}} - {z_1}}}{3}$
$ = \dfrac{{{z_1}}}{3}{e^{ - i\dfrac{\pi }{2}}}$
Now, from the above case, we can say that centroid of the triangle ABC is $\dfrac{{{z_1}}}{3}{e^{ - i\dfrac{\pi }{2}}}$
In the above case, the vertices ABCD are in clock wise, but if the ABCD make an anti-clockwise sequence i.e.

Now in this case B will be ${z_1}{e^{i\dfrac{\pi }{2}}}$ resulting the centroid to be $\dfrac{{{z_1}}}{3}{e^{i\dfrac{\pi }{2}}}$.
From the above results, we can say that centroid of the triangle ABC is $\dfrac{{{z_1}}}{3}{e^{ \pm i\dfrac{\pi }{2}}}$
Using ${e^{i\theta }} = \cos \theta + i\sin \theta $
$ \Rightarrow \dfrac{{{z_1}}}{3}{e^{ \pm i\dfrac{\pi }{2}}} = \dfrac{{{z_1}}}{3}\left( {\cos \left( { \pm \dfrac{\pi }{2}} \right) + i\sin \left( { \pm \dfrac{\pi }{2}} \right)} \right)$
Using $\cos \theta = \cos \left( { - \theta } \right)$and$\sin \left( { - \theta } \right) = - \sin \theta $
$ \Rightarrow \dfrac{{{z_1}}}{3}{e^{ \pm i\dfrac{\pi }{2}}} = \dfrac{{{z_1}}}{3}\left( {\cos \dfrac{\pi }{2} \pm i\sin \dfrac{\pi }{2}} \right)$
Option(D) is correct.
Note: In the above solution we stated that when a point let ${z_k}$ is rotated through an angle $\theta $ with-respect-to origin in the anticlockwise direction then the new point will be${z_k}{e^{i\theta }}$, we apply this formula only when the point is measured with-respect-to origin and both the resultant complex number and the original number is equidistant from the origin and if not then we use the general formula.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




