Question

The breaking stress of a wire depends upon
A. The length of the wire
B. The radius of the wire
C. The material of the wire
D. The shape of the cross-section

Answer 1

Hint: We know that the equation for the relation of stress and strain is $\dfrac{{Stress}}{{Strain}} = \gamma $ . This means that the stress on an object depends on $\gamma $ . Now $\gamma $ as we already know depends upon the material that makes up the wire.

Complete answer:
Before starting the actual solution, it would be good to discuss stress, stress, and their relationship.
Stress – Stress is the force applied per unit area on a material.
Strain – Strain is the change in the dimensions of material when it is under stress.
The relation of stress-strain is given below
$\dfrac{{Stress}}{{Strain}} = \gamma $
Here, $\gamma = $ The proportionality of linear expansion
The stress-strain graph is shown below

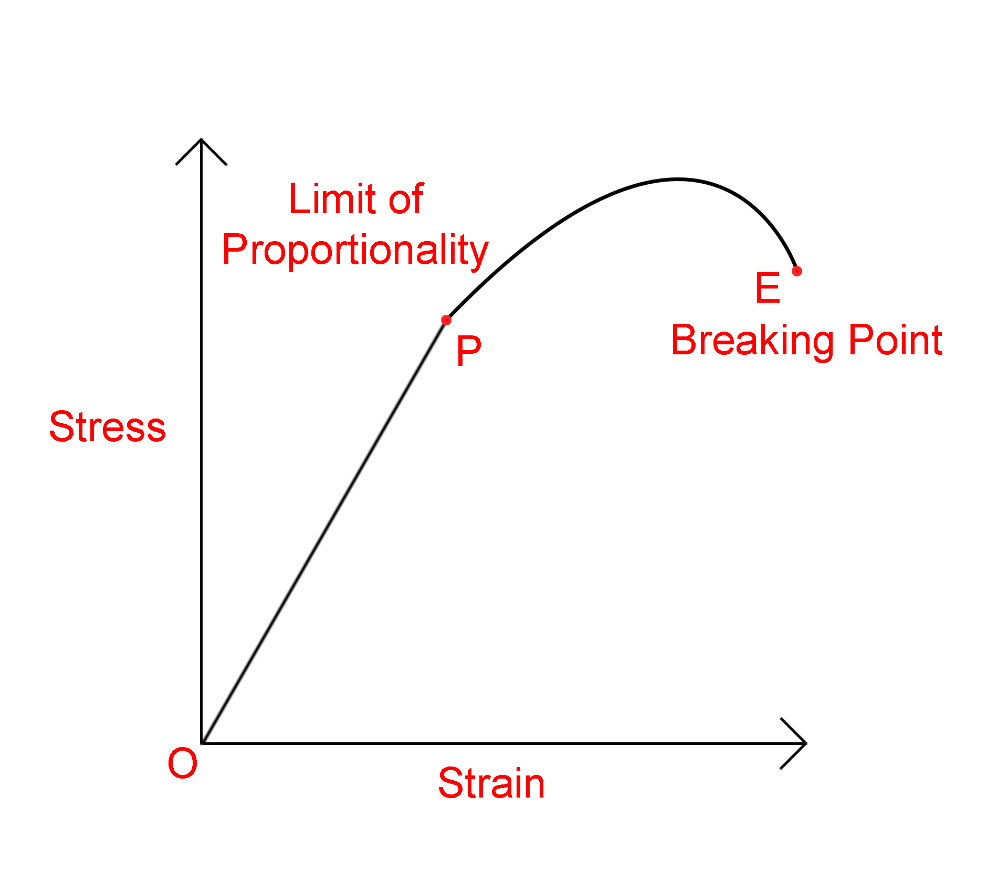
In this graph, you can see the point E which is called the breaking point where the object can longer bear the stress and just breaks into two. At this point even if we reduce the stress the strain still increases.
By the stress-strain equation, i.e. $\dfrac{{Stress}}{{Strain}} = \gamma $ , we can see that the strain of a body does not depend on the length of the wire, the shape of the cross-section of the wire, and the radius of the wire.
 But stress does depend on $\gamma $ . Now $\gamma $ depends on the material of the wire, so the breaking stress also depends on the material of the wire.
In simple words, it means that two objects made of different material will have different breaking stress (the limit of strain the body can bear)

So, the correct answer is “Option C”.

Note:
 The concept of breaking stress that we discussed in the solution above is of great importance to us. Every object that we use whether it be lifts, bridges, mobiles phones, etc. are designed in such a manner that the stress on the object does not exceed the safe limit in normal day to day usage.