Question

The breaking strength of a string is 55 kg wt. The maximum permissible speed of a stone of mass 5kg which is revolved in a vertical circle of radius 4m with the help of this string is $g = 10m/{s^2}$:
A) 10 m/sec.
B) 15 m/sec.
C) 20 m/sec.
D) 25 m/sec.

Answer 1

Hint:Tension is a force working along the length of a medium, especially this force is carried by a flexible medium, like a rope or cable. The tension force pulls outward along the two ends of the string. This Tension in the rope must equal the weight of the supported mass, which can be easily proved using Newton’s second law. Here, the only external forces acting on the mass will be its weight W and the tension T supplied by the rope. Thus, Net force, \[{F_{net}} = T - W = 0\],
where T and W are the magnitudes of the tension and weight and their signs indicate a direction, with up being positive here.

Complete step by step answer:
For a string to help revolve an object without breaking, it should have a tension lower than the maximum tension it can withstand.

Now the maximum tension for the string given in this question for the string is 55 Kg wt.
So, we can write, Tension maximum ${T_{\max }} \leqslant 55g$.

Now, let us consider the figure.
If we consider the stone at a random point A, then the forces acting on this stone are Tension (T) and gravity (mg). Here m= mass of the stone.

     

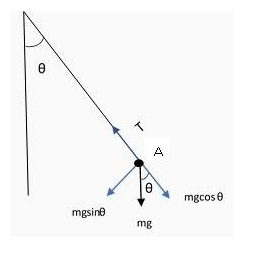
At an angle $\theta $, this gravitational force can be divided into two components, $mg\cos \theta $ and $mg\sin \theta $.
Now, Net force towards the centre will be, Net force,
 \[{F_{net}} = T - mg\cos \theta \].
Also, we know that when a body is moving in a circular motion it will have a centrifugal force that is equal to,
${F_{centri}} = \dfrac{{m{v^2}}}{R}$,
 where m= mass of the body, v= velocity, and R= radius of the circular motion.
So, these two forces, Net force, and the centrifugal force should be equal.
Thus, we can write,
$T - mg\cos \theta = \dfrac{{m{v^2}}}{R}$.
So, we can write,
$T = \dfrac{{m{v^2}}}{R} + mg\cos \theta $. (Equation 1)
Here the maximum value of tension can come when $\cos \theta $ is maximum as all the other terms will be constant. Also, we know that the maximum value $\cos \theta = 1$.
So, now we have from Equation 1, When, $T = {T_{\max }}$ replacing $\cos \theta = 1$,
\[{T_{\max }} = \dfrac{{m{v^2}}}{R} + mg\].
But, according to question,
 ${T_{\max }} \leqslant 55g$.
So, we can write,
\[\dfrac{{m{v^2}}}{R} + mg \leqslant 55g\]
= \[m\left( {\dfrac{{{v^2}}}{R} + g} \right) \leqslant 55g\].
Given in the question, m= 5kg, R= 4m, and $g = 10m/{s^2}$.
So, the equation becomes
\[5\left( {\dfrac{{{v^2}}}{4} + 10} \right) \leqslant 55 \times 10\].
Dividing both sides by 5 we get,
\[\dfrac{{{v^2}}}{4} + 10 \leqslant 11 \times 10\]
= \[\dfrac{{{v^2}}}{4} + 10 \leqslant 110\]
= \[\dfrac{{{v^2}}}{4} \leqslant 110 - 10\]
= \[\dfrac{{{v^2}}}{4} \leqslant 100\]
= \[{v^2} \leqslant 100 \times 4\]
= \[{v^2} \leqslant 400\].
Thus, we can write,
\[v \leqslant \sqrt {400} \]
= \[v \leqslant 20\].
Thus, the maximum permissible speed will be $20m/s$.

So, option (C) is the right answer.

Note: The formula for the centrifugal force ${F_{centri}} = \dfrac{{m{v^2}}}{R}$, where m= mass of the body, v= velocity, and R= radius of the circular motion, is a very important component in solving this problem so we have to remember this formula at all times.