Question

The bob of a simple pendulum has mass 2 g and a charge $ 5.0\mu C $ . It is at rest in a uniform horizontal electric field of intensity $ 2000V/m $ . At equilibrium, the angle that the pendulum makes with the vertical is: (take $ g = 10m/{s^2} $ )
(A) $ {\tan ^{ - 1}}\left( {5.0} \right) $
(B) $ {\tan ^{ - 1}}\left( {2.0} \right) $
(C) $ {\tan ^{ - 1}}\left( {0.5} \right) $
(D) $ {\tan ^{ - 1}}\left( {0.2} \right) $

Answer 1

Hint
To solve this problem, we should consider the force acting on the pendulum bob due to the electric field and the force due to its mass downwards. Since the pendulum is in equilibrium both the forces acting on it can be equated to find the angle that the pendulum makes with the vertical.
The electric force acting on the bob, $ {F_E} = qE $ where $ q $ is the charge in Coulombs and $ E $ is the electric field in $ V/m $ . The force acting on the bob downward due to its gravity, $ F = mg $ where $ m $ is the mass of the bob and $ g $ is the acceleration due to gravity.

Complete step by step answer
Let us assume that, initially the electric field was absent and the only force exerted on the bob will be the downward force due to gravity, as shown in the figure, with the help of dotted lines.

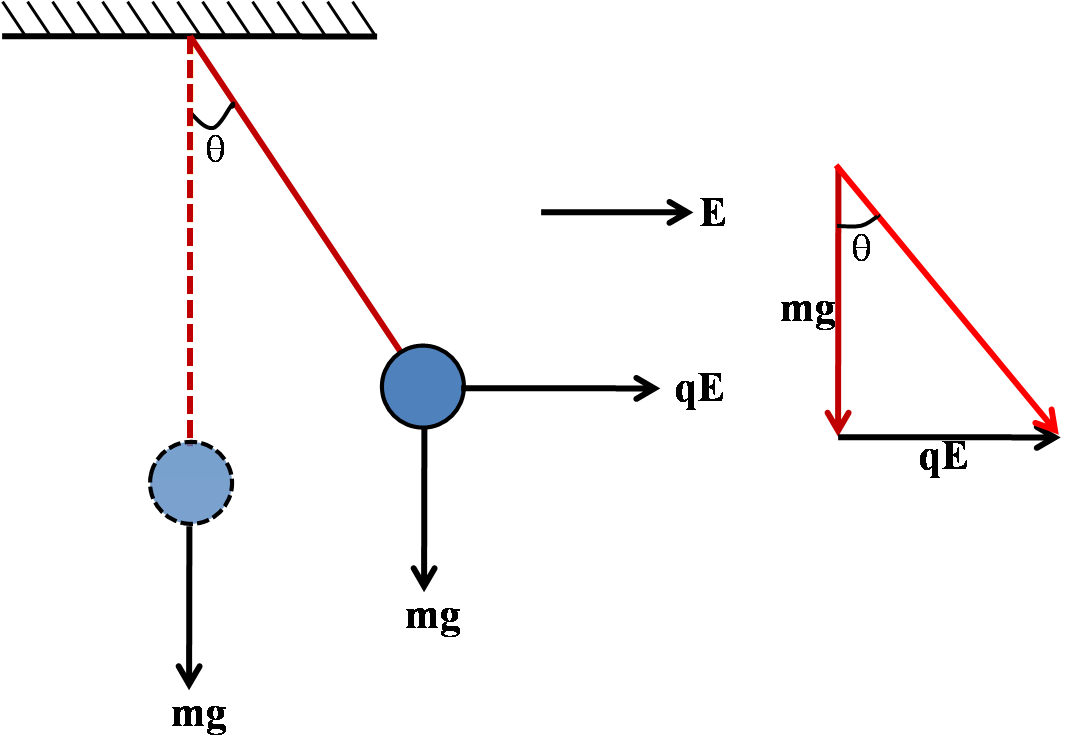
But when the electric field is present, then there is electric force acting on the bob in the horizontal direction. Thus, the bob is displaced from its previous equilibrium position and the new position is represented in the figure with normal line, in which the electric force acting horizontally towards right and the force due to gravity downward acting together to keep the bob in equilibrium. This new equilibrium position is at an angle $ \theta $ as illustrated in figure.
The two forces acting on the bob can be illustrated as the adjacent sides of a triangle as shown in the figure on the right side. Then the triangle forms a right-angled triangle and the angle of the pendulum with the vertical can be estimated as:
 $\Rightarrow \tan \theta = \dfrac{{{\text{opposite side}}}}{{{\text{adjacent side}}}} = \dfrac{{qE}}{{mg}} $
We know that $ q = 5.0\mu C = 5.0 \times {10^{ - 6}}C $ , $ E = 2000V/m $ , $ m = 2.0g = 2.0 \times {10^{ - 3}}kg $ and $ g = 10m/{s^2} $ . Thus, we can substitute these values in the above equation and get,
 $\Rightarrow \tan \theta = \dfrac{{5.0 \times {{10}^{ - 6}}C \times 2000V/m}}{{2.0 \times {{10}^{ - 3}}kg \times 10m/{s^2}}} $
Now, on simplification, we obtain the angle as:
 $\Rightarrow \tan \theta = 0.5 $
Therefore, the angle made by the pendulum would be:
 $\Rightarrow \theta = {\tan ^{ - 1}}\left( {0.5} \right) $
Thus the correct answer is option (C).

Note
We should also note that the resultant of both the forces can be along the hypotenuse of the triangle elucidated from triangle law of vector addition. That means the bob should be moving along the direction of hypotenuse outward. But, since it is given that the pendulum is at rest, the resultant force acting on the bob is zero. This is because, till now we did not consider the tension of the pendulum string which is exactly opposite to the resultant of the other two forces, that is opposite to the hypotenuse of the triangle, and the same magnitude as that of the resultant. Hence, the net external force acting on the bob is zero, and the pendulum is at rest.