Question

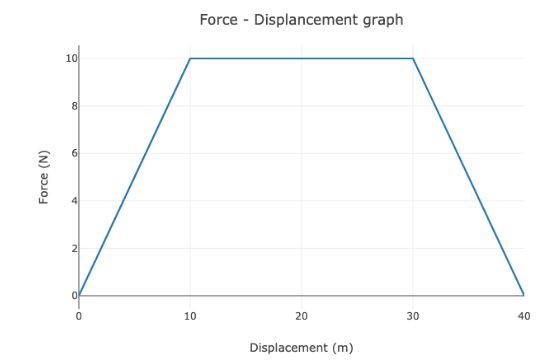
The below figure shows the force-displacement graph for a moving body. What is the work done by the force in displacing the body from x=0 to x=35m?

Answer 1

Hint: In order to solve the question, we will use the concept of area under the graph area under force displacement graph is work done as we have to find the work done of specific part so it can be only done either by adding the by splitting the parts or we can do by subtracting an extra part from the desired part

Formula used:
Area of trapezium = $\dfrac{1}{2} \times h \times (a + b)$
Here, $h$ is the height of trapezium, $a$ is top parallel side of trapezium and $b$ is base parallel side of trapezium.
Area of triangle = $\dfrac{1}{2} \times h \times b$
Here $h$ is the height of the triangle and $b$ is the base of the triangle


Complete step by step answer:
In the question we are given the graph between force and displacement which is for the value of x=0 to x=40m and we have to find the work done by the force in displacing the body from x=0 to x=35m. The area under the force –displacement graph gives the work done. The work done between x=0 to x=40m is the trapezium let the area of the trapezium be ${A_1}$ as we have to find the work done from x=0 to x=35m The work done between x=35m to x=40m is the triangle let the area of the triangle be ${A_2}$.So the work done from x=0 to x=35m be $A = {A_1} - {A_2}$.

Area of trapezium (${A_1}$)= $\dfrac{1}{2} \times h \times (a + b)$
$h = 10 \\
\Rightarrow a = 20 \\
\Rightarrow b = 40$
$\Rightarrow {A_1} = \dfrac{1}{2} \times h \times (a + b)$
$ \Rightarrow {A_1} =\dfrac{1}{2} \times 10 \times (20 + 40)$
$ \Rightarrow {A_1} =300$
Hence the area of trapezium is $300{\text{ }}$.

Area of triangle (${A_2}$)= $\dfrac{1}{2} \times h \times b$
$h = 5\\
\Rightarrow b = 5$
$\Rightarrow {A_2} = \dfrac{1}{2} \times h \times b$
$ \Rightarrow {A_2} =\dfrac{1}{2} \times 5 \times 5$
$ \Rightarrow {A_2} =12.5$
Hence area of triangle is ${\text{12}}{\text{.5 }}$
So the work done from x=0 to x=35m
$A = {A_1} - {A_2}$
$\Rightarrow A = 300 - 12.5$
$\therefore A{\text{ = 287}}{\text{.5 J}}$

Hence the work done from x=0 to x=35 m $A{\text{ = 287}}{\text{.5 J}}$.

Note: Many students will make the mistake by taking the area in meter square but the standard international units of work done are joules so the unit should be considered in joules not square units. There can be other ways to do this question, this the most efficient method with less calculation and step but other ways are correct but can be long.