Question

The below diagram shows a sector OAP of the circle with center O and radius r, containing an angle $\theta $. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of the shaded region is $r\left[ \tan \theta +\sec \theta +\dfrac{\pi \theta }{180}-1 \right]$

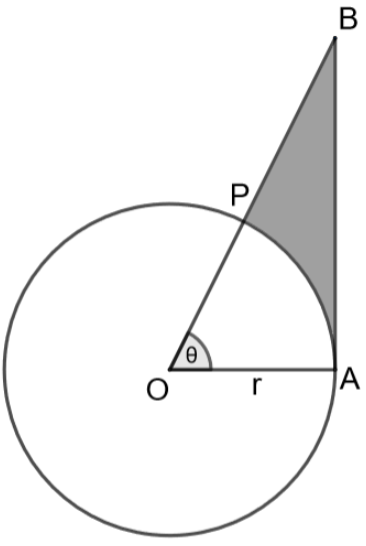
Answer 1

Hint: To solve this question, we should know the basic trigonometric relations between angles and sides of a right-angled triangle. In the question, we can infer that AB is perpendicular to OA which implies that $\Delta OAB$ is a right-angled triangle. We can infer that for the given angle $\theta $, the side AB is the opposite side, the side OA is the adjacent side and OB is the hypotenuse. We can write that $\tan \theta =\dfrac{\text{Opposite side}}{\text{Adjacent side}}=\dfrac{AB}{OA}=\dfrac{AB}{r}$ and $\sec \theta =\dfrac{\text{Hypotenuse}}{\text{Adjacent side}}=\dfrac{OB}{OA}=\dfrac{OB}{r}$. We know that the required perimeter is the sum of the lengths of AB, PB, arc PA. We can get the length AB from the above relations, PB from the relation that $PB=OB-OP=OB-r$. The length of the arc of a circle of radius r and the included angle $\theta $ is given by the formula $\text{arc length}=\dfrac{\theta }{{{360}^{\circ }}}\times 2\pi r$. By summing up the values, we will get the required perimeter.

Complete step-by-step solution:

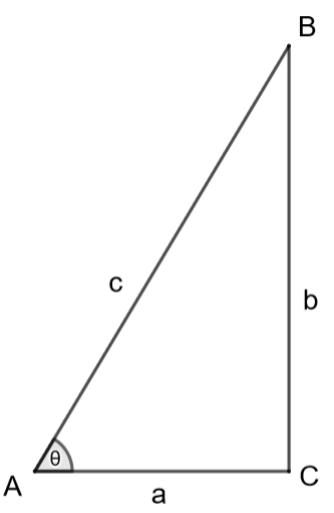
For the given triangle ABC, the angle $\angle A=\theta $ and angle $\angle C={{90}^{\circ }}$. We can infer that the triangle is a right-angled triangle.
For the given angle $\theta $, we can write that AC = a is the adjacent side, BC = b is the opposite side and AB = c is the hypotenuse.
From the basic definitions of trigonometric t=ratios, we can write that
$\tan \theta =\dfrac{\text{Opposite side}}{\text{Adjacent side}}=\dfrac{b}{a}$
$\sec \theta =\dfrac{\text{Hypotenuse}}{\text{Adjacent side}}=\dfrac{c}{a}$

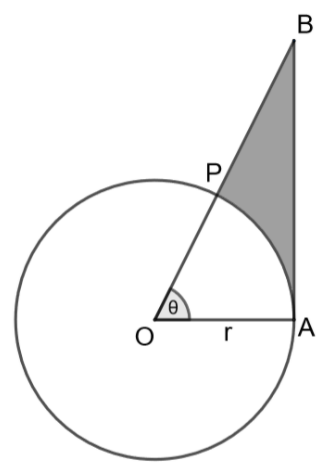
Let us consider the triangle OAB from the above diagram,
As given in the question, we can write that angle $\angle A={{90}^{\circ }}$, the triangle is a right angled triangle. For the given angle $\theta $, we can write that the side AB is opposite side, the side OA is adjacent side and OB is hypotenuse. We can write that
$\begin{align}
  & \tan \theta =\dfrac{\text{Opposite side}}{\text{Adjacent side}}=\dfrac{AB}{OA}=\dfrac{AB}{r} \\
 & AB=r\tan \theta \to \left( 1 \right) \\
\end{align}$
$\begin{align}
  & \sec \theta =\dfrac{\text{Hypotenuse}}{\text{Adjacent side}}=\dfrac{OB}{OA}=\dfrac{OB}{r} \\
 & OB=r\sec \theta \to \left( 2 \right) \\
\end{align}$
The length of the arc of a circle of radius r and the included angle $\theta $ is given by the formula $\text{arc length}=\dfrac{\theta }{{{360}^{\circ }}}\times 2\pi r$.
The length of the arc PA which includes an angle $\theta $ at the centre is
$PA=\dfrac{\theta }{{{360}^{\circ }}}\times 2\pi r=\dfrac{{{\theta }^{\circ }}}{180}\times \pi r\to \left( 3 \right)$
We can write the length of the side PB as $PB=OB-OP$
As we know that OP = r, we can write that
$PB=OB-r\to \left( 4 \right)$
We know that the required perimeter is the sum of AB, PB, arc PA. Mathematically,
$Perimeter=AB+PB+arc\left( PA \right)$
From the equations 1, 2, 3, 4, we can write that
$\begin{align}
  & Perimeter=r\tan \theta +OB-r+\dfrac{{{\theta }^{\circ }}}{180}\times \pi r \\
 & Perimeter=r\tan \theta +r\sec \theta -r+\dfrac{{{\theta }^{\circ }}}{180}\times \pi r \\
\end{align}$
By taking r common in the whole R.H.S, we get that
$\begin{align}
  & Perimeter=r\left( \tan \theta +\sec \theta +\dfrac{{{\theta }^{\circ }}}{180}\times \pi -1 \right) \\
 & Perimeter=r\left( \tan \theta +\sec \theta +\dfrac{\pi {{\theta }^{\circ }}}{180}-1 \right) \\
\end{align}$
$\therefore $ Hence proved that the required perimeter is $Perimeter=r\left( \tan \theta +\sec \theta +\dfrac{\pi {{\theta }^{\circ }}}{180}-1 \right)$.

Note: Students can make a mistake while calculating the length of the arc by taking 180 in place of 360 because of a small confusion. To avoid this, the trick is to remember that circle is also an arc of angle ${{360}^{\circ }}$ and circumference is $2\pi r$. We can infer that for an angle of ${{360}^{\circ }}$, the perimeter is $2\pi r$, then for an angle of $\theta $we can apply the unitary method and get the formula for the length of the arc as $\dfrac{\theta }{{{360}^{\circ }}}\times 2\pi r$.