Question

The base of an equilateral triangle is the line x + y = 2 and vertex to opposite to this side A(2,-1). Find the equation of side AB and AC.

Answer 1

Hint: In this question, we are given an equilateral triangle with coordinates of one vertex A. and we are also given an equation of a line of the base. We have to find the linear equations of the other two sides i.e. AB and AC. We also know that all angles of an equilateral triangle is ${{60}^{\circ }}$. We will also use slope-intercept form in this question.

Complete step by step solution:
Now, let’s begin to solve the question.

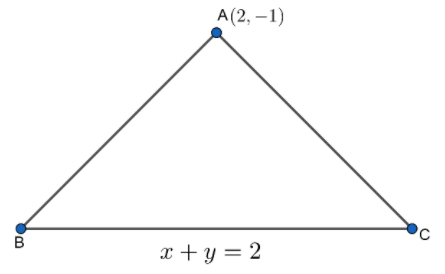
We are given an equilateral triangle $\Delta ABC$ which has all sides equal and all angles of ${{60}^{\circ }}$each. We are given the equation of base BC = x + y = 2 and coordinate of A(2,-1).
First convert the given equation of base in the slope intercept form.
$\Rightarrow x+y=2$
Slope intercept form:
$y=-x+2$
Here the slope ${{m}_{1}}$ = -1. Let the slope of AB be ${{m}_{2}}$. If we have to find ${{m}_{2}}$, we will apply the formula:
 tan$\theta =\dfrac{|{{m}_{1}}-{{m}_{2}}|}{|1+{{m}_{1}}{{m}_{2}}|}$
Here, $\theta ={{60}^{\circ }},{{m}_{1}}=-1$
Place the values in the formula:
tan${{60}^{\circ }}=\dfrac{|-1-{{m}_{2}}|}{|1+\left( -1 \right){{m}_{2}}|}$
value of tan${{60}^{\circ }}=\sqrt{3}$
$\sqrt{3}=\dfrac{|-1-{{m}_{2}}|}{|1-{{m}_{2}}|}$
Remove the modulus sign:
$\sqrt{3}=\pm \dfrac{-1-{{m}_{2}}}{1-{{m}_{2}}}$
For positive value:
$\Rightarrow \sqrt{3}=\dfrac{-1-{{m}_{2}}}{1-{{m}_{2}}}$
Take denominator to the other side of the equation:
$\Rightarrow \sqrt{3}\left( 1-{{m}_{2}} \right)=-1-{{m}_{2}}$
Open the bracket and multiply:
$\Rightarrow \sqrt{3}-\sqrt{3}{{m}_{2}}=-1-{{m}_{2}}$
Take constants on one side:
$\Rightarrow {{m}_{2}}-\sqrt{3}{{m}_{2}}=-1-\sqrt{3}$
Take ${{m}_{2}}$ common:
$\Rightarrow {{m}_{2}}\left( 1-\sqrt{3} \right)=-1-\sqrt{3}$
Solve for ${{m}_{2}}$:
$\therefore {{m}_{2}}=\dfrac{-1-\sqrt{3}}{1-\sqrt{3}}$
For negative value:
$\Rightarrow \sqrt{3}=-\left( \dfrac{-1-{{m}_{2}}}{1-{{m}_{2}}} \right)$
$\Rightarrow \sqrt{3}=\dfrac{1+{{m}_{2}}}{1-{{m}_{2}}}$
Take denominator to the other side of the equation:
$\Rightarrow \sqrt{3}\left( 1-{{m}_{2}} \right)=1+{{m}_{2}}$
Open the bracket and multiply:
$\Rightarrow \sqrt{3}-\sqrt{3}{{m}_{2}}=1+{{m}_{2}}$
Take constants on one side:
$\Rightarrow \sqrt{3}-1={{m}_{2}}+\sqrt{3}{{m}_{2}}$
Take ${{m}_{2}}$ common:
$\Rightarrow \sqrt{3}-1={{m}_{2}}\left( 1+\sqrt{3} \right)$
Solve for ${{m}_{2}}$:
$\therefore {{m}_{2}}=\dfrac{\sqrt{3}-1}{\sqrt{3}+1}$
Now, we will use one value of ${{m}_{2}}$for AB side and another value of ${{m}_{2}}$ for AC side because slopes will be equal for both sides.
If we are given a point say $\left( {{x}_{1}},{{y}_{1}} \right)$ and a slope ‘m’, then equation of a line can be obtained as:
$\Rightarrow y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
Here also we are given a point A(2,-1) and a slope.
So for side AB, we will take point A(2,-1) and slope ${{m}_{2}}=\dfrac{-1-\sqrt{3}}{1-\sqrt{3}}$, so the equation will be:
$\Rightarrow y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
Place all the values:
$\Rightarrow y+1=\dfrac{-1-\sqrt{3}}{1-\sqrt{3}}\left( x-2 \right)$
The above equation is for side AB.
Now, for side AC, we will take point A(2,-1) and slope ${{m}_{2}}=\dfrac{\sqrt{3}-1}{\sqrt{3}+1}$, so the equation will be:
$\Rightarrow y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
Place all the values:
$\Rightarrow y+1=\dfrac{\sqrt{3}-1}{\sqrt{3}+1}\left( x-2 \right)$
The above equation is for side AC.

Note: You can leave the equations in root itself, there is no need to solve further. You should remember all the trigonometric ratios for finding angles for triangles. Slope intercept form makes the equation much easier to solve. So you should know all the concepts related to it. The slope intercept form is y = mx + c where m is the slope of a line.