Question

The base of a right pyramid is a regular hexagon whose area is 243 square cm. If the area of a side face of the pyramid is 46 square cm, what should be its volume (in cc.) in the nearest integer value? \[\]

Answer 1

Hint: We use formula for volume of pyramid $V=\dfrac{1}{3}bh$ where $b$ is that area of base and $h$ is height of pyramid. We are given $b=243$ and we have to find only $h$. We use the formula $6\times \dfrac{\sqrt{3}}{4}{{a}^{2}}$ for the area of regular hexagon and find its side $a$ of side face. We find apothem $p$ of regular hexagon as $p=\dfrac{\sqrt{3}}{2}a$ and the slant height of the pyramid using the given area of area of side face. We find the height of pyramid $h=\sqrt{{{l}^{2}}-{{p}^{2}}}$. \[\]

Complete step by step answer:
We know that a Pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a lateral face. A right pyramid has its apex directly above the centroid of its base. A pyramid that has a regular polygon base is called a regular pyramid.
The volume of pyramid is given with $b$ as the area of the base and $h$ as the height of from the base to the apex also is given as
\[V=\dfrac{1}{3}bh\]
We are given the question that the base of a right pyramid is a regular hexagon whose area is 243 square cm which means $b=243$ square cm. The area of a side face of the pyramid is 46 square cm. We draw the rough figure of it below with O as the apex and ABCDEF as the base of a regular hexagonal base.
 

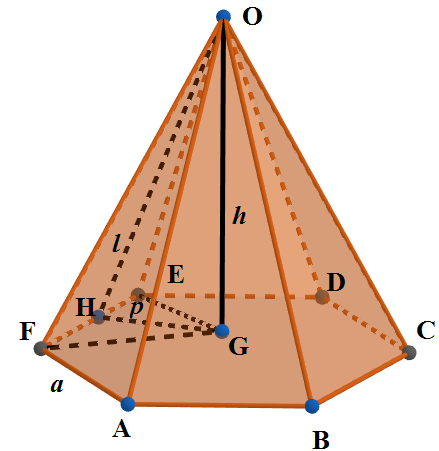
Here $l$ is the slant height dropped from apex on one of the sides (Here OH). The line segment GH is called apothem whose length we denote as $p$. \[\]
We know that area of regular hexagon with side $a$ is 6 times the area of equilateral triangle with side $a$ which means $6\times \dfrac{\sqrt{3}}{4}{{a}^{2}}$. So we have;
\[\begin{align}
  & 6\times \dfrac{\sqrt{3}}{4}{{a}^{2}}=243 \\
 & \Rightarrow {{a}^{2}}=\dfrac{243}{6}\times \dfrac{4}{\sqrt{3}} \\
 & \Rightarrow {{a}^{2}}=\dfrac{162}{\sqrt{3}}=93.53 \\
 & \Rightarrow a=9.67 \\
\end{align}\]
We observe the triangle OEF which is a die face of the pyramid with slant height $l=OH$ and base $a=EF=9.67$cm. We are given its area as 46 square cm. So we have;
\[\begin{align}
  & \dfrac{1}{2}\times l\times a=46 \\
 & \Rightarrow l=\dfrac{46\times 2}{a} \\
 & \Rightarrow l=\dfrac{92}{9.67}=9.81 \\
\end{align}\]
We can find the apothem $p$ as the height of equilateral triangle EGF as
\[p=\dfrac{\sqrt{3}}{2}a=\dfrac{\sqrt{3}}{2}\times 9.67=8.37\]
We use Pythagoras theorem in right angled triangle OGH to have;
\[\begin{align}
  & h=\sqrt{{{l}^{2}}-{{p}^{2}}} \\
 & \Rightarrow h=\sqrt{{{9.81}^{2}}-{{8.37}^{2}}} \\
 & \Rightarrow h=5.12 \\
\end{align}\]
So the volume of pyramid cubic cm is
\[V=\dfrac{1}{3}bh=\dfrac{1}{3}\times 243\times 5.12=414.44\]

We round off to the nearest integer and have the volume of the pyramid as 414 cubic cm. \[\]

Note: We can alternatively solve using the base area with the apothem and side as $3pa$ and then the volume $pah$. Apothem is the perpendicular dropped from the centre of a regular polygon to the side. The regular polygon with $n$ sides at the centre divides the interior of the polygon into $n$ equilateral l triangles.