Question

The back and forth motion of an object is called:
A. vibration
B. rotation
C. translation
D. linear motion

Answer 1

Hint: In this question, we will first see the definition of vibration and then see the difference between vibration and oscillation. After this we see the examples of oscillation motion. At last, we will see about the simple harmonic motion.

Complete answer:
Let us first see definition of vibration or oscillation:
The back and forth motion of the object is called vibration or oscillation. The mean position about which the body oscillates is called the equilibrium position.
If the body is given a small displacement from the position, a force comes into play which tries to bring the body back to the equilibrium point, giving rise to oscillations or vibrations.

For example, a ball placed in a bowl will be in equilibrium at the bottom. If displaced a little from the point, it will perform oscillations in the bowl. Every oscillatory motion is periodic, but every periodic motion need not be oscillatory. Circular motion is a periodic motion, but it is not oscillatory.

There is no significant difference between oscillations and vibrations. It seems that when the frequency is small, we call it oscillation (like the oscillation of a branch of a tree), while when the frequency is high, we call it vibration (like the vibration of a string of a musical instrument).

Let us see about Simple harmonic motion:
Simple harmonic motion is the simplest form of oscillatory motion. This motion arises when the force on the oscillating body is directly proportional to its displacement from the mean position, which is also the equilibrium position.

Let us consider a particle vibrating back and forth about the origin of an x-axis between the limits +A and –A as shown in figure. In between these extreme positions the particle figure.

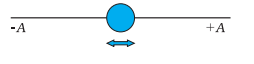
Fig: The particle vibrates back and forth about the equilibrium position between two extremes +A and –A.
A particle vibrating back and forth about the origin of x-axis, between the limits +A and –A. moves in such a manner that its speed is maximum when it is at the origin and zero when it is at ± A. The time t is chosen to be zero when the particle is at +A and it returns to +A at t = T

So, the correct answer is “Option A”.

Note:
At any point in its oscillation, this force is directed towards the mean position. In practice, oscillating bodies eventually come to rest at their equilibrium positions, because of the damping due to friction and other dissipative causes. A moving pendulum is also an example of the oscillatory motion.