Question

The auxiliary circle of a hyperbola is defined as:
$(a)$ The auxiliary circle of a hyperbola is a circle with its center on the polar and contains the two vertices.
$(b)$ The circle whose center concurs with that of the ellipse and whose radius is equal to the ellipse’s semi major axis.
$(c)$ The auxiliary circle for a hyperbola is a circle with its center on the axis and contains the two vertices.
$(d)$ None of these

Answer 1

Hint: Use the general equation of hyperbola as $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$, where the center of the hyperbola is (0, 0) and the length of the transverse axis and conjugate axis is (2a) and (2b), along with the basics of auxiliary circle to get the equation of auxiliary circle to this hyperbola. This will help finding the right option.

Complete Step-by-Step solution:
The Auxiliary circle of a hyperbola is defined as the circle with the center same as the hyperbola and with transverse axis as its diameter. The endpoints of the transverse axis are the two vertices of the hyperbola, so the circle also contains the two vertices of the hyperbola.

Let the equation of hyperbola is
$\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$
Where the center of the hyperbola is (0, 0) and the length of the transverse axis and conjugate axis is (2a) and (2b), as we know transverse axis is along x-axis and conjugate axis is along y-axis.
So according to the definition of auxiliary circle the center and diameter of the circle is (g, f) = (0, 0) and (d = 2a) respectively.
Now as we know the radius (r) of the circle is half of the diameter (d).
$ \Rightarrow r = \dfrac{d}{2} = \dfrac{{2a}}{2} = a$.
So the general equation of circle is
$ \Rightarrow {\left( {x - g} \right)^2} + {\left( {y - f} \right)^2} = {r^2}$
$ \Rightarrow {x^2} + {y^2} = {a^2}$
So this is the required auxiliary circle of a hyperbola.
Hence option (C) is correct.

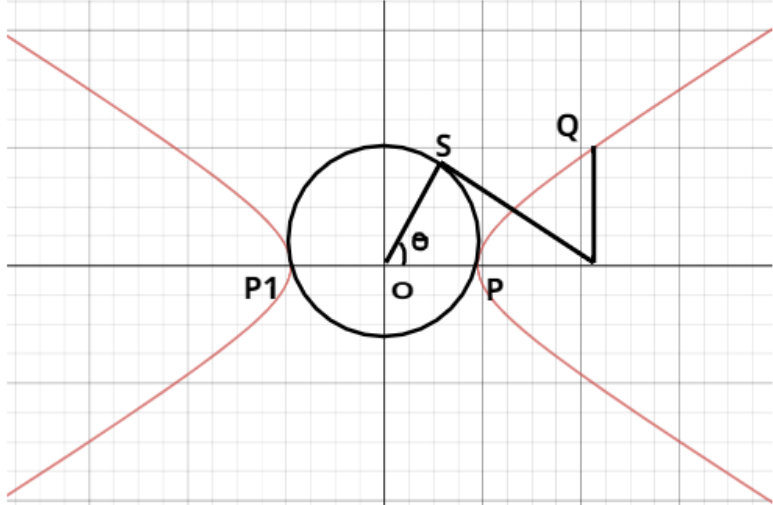
Note: A circle drawn with center O and $P1P$ as diameter is called the auxiliary circle of the hyperbola. Equation of the auxiliary circle of a hyperbola is ${x^2} + {y^2} = {a^2}$. Key point is that from the figure we can see that points Q and S are called the corresponding points on the hyperbola and the auxiliary circle respectively. The point P has the coordinates $Q(a\sec \theta ,\tan \theta )$, where $\theta $ is called the eccentric angle.