Question

The areas of three adjacent faces of a rectangular box which meet in a point are known. The product of these areas is equal to \[\]
A. the volume of the box \[\]
B. twice the volume of the box \[\]
C. the square of the volume of the box \[\]
D. the cube root of the volume of the box \[\]

Answer 1

Hint: We denote the denote the vertices of the cuboid shaped rectangular box as A, B, C, D, E, F, G, H and three different sides length, breadth and height denoted $l,$$b$ and $h$. We find surface area of any three adjacent surfaces using the formula for area of a rectangle and find their product. We compare the product with volume of the cuboid box $V=lbh$ to choose the correct option. \[\]

Complete step by step answer:
We know that a cuboid is a three dimensional object with six rectangular faces joined by 8 vertices. It has three different types of sides called length, breadth and height denoted $l,$$b$ and $h$. \[\]
The amount of space contained by a three dimensional object is measured by the quantity called volume. The amount of space that is occupied by a cuboid is the product of length, breadth and height. Mathematically, volume denoted as $V$of a cuboid is
\[V=l\times b\times h=lbh....\left( 1 \right)\]

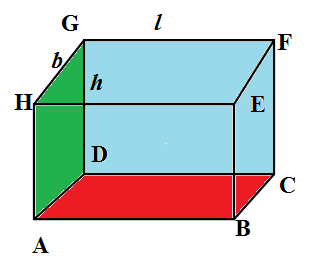
 Let us denote the vertices of the cuboid as A, B, C, D, E, F, G, H. We are going to call two rectangular surfaces adjacent when they share a common vertex. We have the rectangular surfaces ABCD, DCFG and ADGH share the common vertex D. Let us assign
\[\begin{align}
  & AB=HE=GF=CD=l \\
 & AD=BC=EF=GH=b \\
 & AH=GD=BE=CF=h \\
\end{align}\]
We are given the question that the areas of three adjacent faces of a rectangular box which meet in a point are known. The rectangular face is the product of its different sides. So the areas of three adjacent faces are
\[\begin{align}
  & \text{Area of }ABCD=AB\times BC=l\times b=lb \\
 & \text{Area of }DCFG=DC\times GD=h\times l=hl \\
 & \text{Area of }ADGH=GH\times GD=l\times b=lb \\
\end{align}\]
So the product surface areas of the three adjacent faces is
\[\begin{align}
  & \text{Area of }ABCD\times \text{Area of }ABCD\times \text{Area of }ABCD \\
 & =lb\times bh\times hl={{l}^{2}}{{b}^{2}}{{h}^{2}}={{\left( lbh \right)}^{2}} \\
\end{align}\]
.We use value for equation (1) and have;
\[\text{Area of }ABCD\times \text{Area of }ABCD\times \text{Area of }ABCD={{\left( lbh \right)}^{2}}={{V}^{2}}\]
The product of these areas is equal to the square of the volume.

So, the correct answer is “Option C”.

Note: A cube is cuboid with all sides of equal length which means $l=b=h=a$ and unlike the areas of the faces of a cuboid , the areas of faces of the cube are equal. The total surface area of the rectangular box will be $2\left( lb+bh+hl \right)$and length of the space diagonal will be $\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}$.The total surface of cube is $6{{a}^{2}}$ and the volume is ${{a}^{3}}$.