Question

The area under a force time graph gives acceleration.
A. True
B. False

Answer 1

Hint: Area under the force-time graph gives the impulse acting on the body.

Complete step by step solution:
Let us consider a Force time graph shown below with peak of force as \[{F_{peak}}\]. The x-axis Force makes the curve OAB such that a triangle OAB is formed.

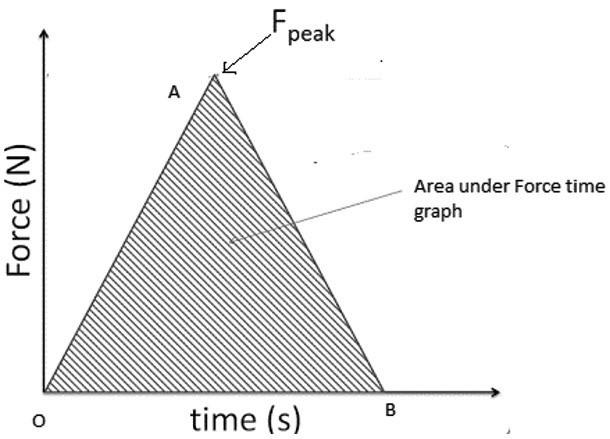
If we calculate area of triangle OAB,
 Area of shaded portion \[ = {\text{ }}\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/
 \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} {\text{ }}Base \times Altitude\]
                                             \[ = \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/
 \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} {\text{ }}T \times {F_{peak}} = Formula{\text{ }}of{\text{ }}Impulse = \] Change in momentum of body

Hence, Area under the force-time graph gives the impulse (or change in momentum) acting on the body.
Thus, the above statement that the area under the Force time graph gives acceleration is false.

Additional Information:
1. The dimensional formula of impulse is the same as that of momentum \[\left[ {M{\text{ }}L{\text{ }}{T^{ - 1}}} \right]\]. In SI the unit of impulse is Ns or\[kgm{s^{ - 1}}\].
2. An accelerated motion is always due to a force. The acceleration produced by a force in the motion of a body depends only upon its mass.


Note: Impulse received during an impact is equal to the product of average force during the impact and the time for which the impact lasts and is also equal to the change in momentum produced during the impact.