Question

The area of the triangle formed by the points whose position vectors are \[3i+j\] , \[5i+2j+k\] , \[i-2j+3k\] .
(A) \[\sqrt{23}\] sq units
(B) \[\sqrt{21}\] sq units
(C) \[\sqrt{29}\] sq units
(D) \[\sqrt{33}\] sq units

Answer 1

Hint: The position vectors of point A, B, and C are \[3i+j\] , \[5i+2j+k\] , and \[i-2j+3k\] . We know the formula that if we have three vectors \[\overrightarrow{A}\] , \[\overrightarrow{B}\] , and \[\overrightarrow{C}\] . Then, the area of \[\Delta ABC\] is given by the half of the vector product of \[\left( \overrightarrow{A}-\overrightarrow{C} \right)\] and \[\left( \overrightarrow{B}-\overrightarrow{C} \right)\] . Use this formula and calculate the area in vector form. Now, get the magnitude of the area vector using the formula that magnitude of a vector \[xi+yj+zk\] is \[\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}\] .

Complete step by step answer:
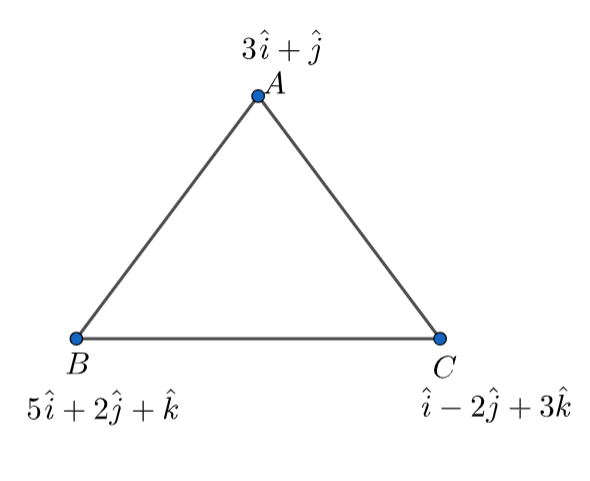
According to the question, we are given the position vectors of three points and we have to calculate the area of the triangle.
Let us assume that A, B, and C are the points.
The position vector of point A = \[\overrightarrow{A}=3i+j\] …………………………………………….(1)
The position vector of point B = \[\overrightarrow{B}=5i+2j+k\] …………………………………………….(2)
The position vector of point C = \[\overrightarrow{C}=i-2j+3k\] …………………………………………….(3)
Here, we are asked to find the area of \[\Delta ABC\] .

We know the formula that if we have three vectors \[\overrightarrow{A}\] , \[\overrightarrow{B}\] , and \[\overrightarrow{C}\] . Then, the area of \[\Delta ABC\] is given by the half of the vector product of \[\left( \overrightarrow{A}-\overrightarrow{C} \right)\] and \[\left( \overrightarrow{B}-\overrightarrow{C} \right)\] i.e.,
The area of \[\Delta ABC\] = \[\dfrac{1}{2}\left[ ~\left( \overrightarrow{A}-\overrightarrow{C} \right)\times \left( \overrightarrow{B}-\overrightarrow{C} \right) \right]\] ………………………………..(4)
From equation (1), and equation (3), we get
\[\left( \overrightarrow{A}-\overrightarrow{C} \right)=\left( 3i+j \right)-\left( i-2j+3k \right)=\left( 3-1 \right)i+\left( 1+2 \right)j-3k=2i+3j-3k\] ………………………………………….(5)
Similarly, from equation (2), and equation (3), we get
\[\left( \overrightarrow{B}-\overrightarrow{C} \right)=\left( 5i+2j+k \right)-\left( i-2j+3k \right)=\left( 5-1 \right)i+\left( 2+2 \right)j+\left( 1-3 \right)k=4i+4j-2k\] ………………………………………….(6)
Now, from equation (4), equation (5), and equation (6), we get
The area of \[\Delta ABC\] = \[\dfrac{1}{2}\times \left[ \left( 2i+3j-3k \right)\times \left( 4i+4j-2k \right) \right]\] ……………………………………….(7)
We know the property that \[i\times i=0\] , \[j\times j=0\] , \[k\times k=0\] , \[i\times j=k\] , \[i\times k=-j\] , \[j\times i=-k\] ,
\[j\times k=i\] , \[k\times i=j\] , and \[k\times j=-i\] ……………………………………..(8)
Now, using equation (8) and on simplifying equation (7), we get
The area of \[\Delta ABC\] = \[\dfrac{1}{2}\times \left[ 6i-8j-4k \right]\] = \[3i-4j-2k\] ……………………………………….(9)
We know the formula for the magnitude of a vector \[xi+yj+zk\] , Magnitude = \[\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}\] …………………………………………………(10)
Now, from equation (9) and equation (10), we get
The area of \[\Delta ABC\] = \[\sqrt{{{3}^{2}}+{{\left( -4 \right)}^{2}}+{{\left( -2 \right)}^{2}}}=\sqrt{9+16+4}=\sqrt{29}\] sq units.
Therefore, the area of the triangle is \[\sqrt{29}\] sq units.
Hence, the correct option is C .

Note:
For solving this type of question, one must remember the formula for the area of the triangle. That is, the area of the triangle enclosed by the position vectors \[\overrightarrow{A}\] , \[\overrightarrow{B}\] , and \[\overrightarrow{C}\] is equal to the vector product of \[\left( \overrightarrow{A}-\overrightarrow{C} \right)\] and \[\left( \overrightarrow{B}-\overrightarrow{C} \right)\] .