Question

The area of the quadrilateral formed by the foci of the hyperbolas $\dfrac{{{{\text{x}}^2}}}{{{{\text{a}}^2}}} + \dfrac{{{{\text{y}}^2}}}{{{{\text{b}}^2}}} = 1\;and\;\dfrac{{{{\text{x}}^2}}}{{{{\text{a}}^2}}} + \dfrac{{{{\text{y}}^2}}}{{{{\text{b}}^2}}} = - 1\;is - $
$\begin{align}
  &{\text{A}}.\;4\left( {{{\text{a}}^2} + {{\text{b}}^2}} \right) \\
  &{\text{B}}.\;2\left( {{{\text{a}}^2} + {{\text{b}}^2}} \right) \\
  &{\text{C}}.\;\left( {{{\text{a}}^2} + {{\text{b}}^2}} \right) \\
  &{\text{D}}.\;\dfrac{1}{2}\left( {{{\text{a}}^2} + {{\text{b}}^2}} \right) \\
\end{align} $

Answer 1

Hint: In this question the concept of conic sections and their foci will be used. A hyperbola is a conic. Hyperbola is a locus of the point in the plane with a constant ratio of the difference between the distance from the two fixed points termed foci. The coordinates of the foci of a general hyperbola are-
$For\;\dfrac{{{{\text{x}}^2}}}{{{{\text{a}}^2}}} + \dfrac{{{{\text{y}}^2}}}{{{{\text{b}}^2}}} = 1,\;{\text{F}}\left( { \pm ae,0} \right)\;where\;{\text{e}} = \sqrt {1 + \dfrac{{{{\text{b}}^2}}}{{{{\text{a}}^2}}}} $
$For\;\dfrac{{{{\text{x}}^2}}}{{{{\text{a}}^2}}} + \dfrac{{{{\text{y}}^2}}}{{{{\text{b}}^2}}} = - 1,\;{\text{F}}\left( {0,\; \pm be} \right)where\;{\text{e}} = \sqrt {1 + \dfrac{{{{\text{a}}^2}}}{{{{\text{b}}^2}}}} $

Complete step-by-step solution -

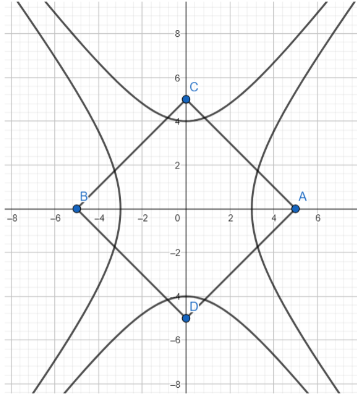
Let the four foci be $A(a{e_1}, 0), B(-a{e_1}, 0), C(0, b{e_2}) and D(0, -b{e_2})$.
From the given formulas, we can write that-
$\begin{align}
  &{{\text{e}}_1} = \sqrt {1 + \dfrac{{{{\text{b}}^2}}}{{{{\text{a}}^2}}}} = \dfrac{{\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} }}{{\text{a}}} \\
  &a{e_1} = \sqrt {{{\text{a}}^2} + {{\text{b}}^2}} \\
  &{{\text{e}}_2} = \sqrt {1 + \dfrac{{{{\text{a}}^2}}}{{{{\text{b}}^2}}}} = \dfrac{{\sqrt {{{\text{b}}^2} + {{\text{a}}^2}} }}{{\text{b}}} \\
  &b{e_2} = \sqrt {{{\text{a}}^2} + {{\text{b}}^2}} \\
\end{align} $
So, the coordinates of the foci are-
${\text{A}}\left( {\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} ,\;0} \right),\;{\text{B}}\left( { - \sqrt {{{\text{a}}^2} + {{\text{b}}^2}} ,\;0} \right),\;{\text{C}}\left( {0,\;\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} } \right)\;and\;{\text{D}}\left( {0, - \sqrt {{{\text{a}}^2} + {{\text{b}}^2}} } \right)$
 From the figure, we can see that the diagonals AB and CD are perpendicular to each other as they lie along the coordinate axes. Also, they are equal in length having a length of $\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} - \left( { - \sqrt {{{\text{a}}^2} + {{\text{b}}^2}} } \right) = 2\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} $
So, the quadrilateral formed is a square. To find its area, we need to find the length of its side. Let the origin be O, we can apply pythagoras theorem in triangle OAC as-
$\begin{align}
  &O{A^2} + O{C^2} = A{C^2} \\
  &{\left( {\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} } \right)^2} + {\left( {\sqrt {{{\text{a}}^2} + {{\text{b}}^2}} } \right)^2} = A{C^2} \\
  &{{\text{a}}^2} + {{\text{b}}^2} + {{\text{a}}^2} + {{\text{b}}^2} = A{C^2} \\
  &2\left( {{{\text{a}}^2} + {{\text{b}}^2}} \right) = A{C^2} \\
  &AC = \sqrt {2\left( {{{\text{a}}^2} + {{\text{b}}^2}} \right)} \\
\end{align} $
In order to find the area of the square, we need to find the square of its side as-
$Area = {\left( {side} \right)^2}$
$Area = {\left( {AC} \right)^2}$
$Area = {\left( {\sqrt {2\left( {{{\text{a}}^2} + {{\text{b}}^2}} \right)} } \right)^2} = 2\left( {{{\text{a}}^2} + {{\text{b}}^2}} \right)\;units$
This is the required answer, the correct option is B.

Note: In such types of questions, we need to apply multiple concepts ranging from conics to triangles. We must have detailed knowledge about a hyperbola, its properties, eccentricity, and its foci. Also, we must always draw a relevant diagram which helps us better understand the question. We must remember to write the units, even if they are not mentioned in the question.