Question

The area of cross-section of a pipe is 10.4 sq. cm and water is running through it at the rate of 54 km/h. If the pipe is always 60% full, find the volume of water, in liters, that flows through the pipe in 5 minutes.​

Answer 1

Hint: -First of all, we will convert the rate of flow of water from km/hr to m/sec as follows
It is given that the rate of flow of water is 54 km/hr, so, we can convert this into m/sec as follows
\[\begin{align}
  & =54\times \dfrac{5}{18} \\
 & =15\ m/\sec \\
\end{align}\]

Complete step-by-step answer:
Now, in this question, we can analyze the question better by taking an instant of time which can be 1 second
Now, as the pipe is cylindrical in shape, we can see that the height of the cylindrical pipe will be 15m because as we are taking a second into consideration, so, in that second water will move 15m (from the rate of flow of water) and the length that is will cover would become the height of the pipe.
Also, it is given in the question that the area of cross-section of the pipe is 10.4 sq. cm.
As mentioned in the question, we have to find the volume of water that comes out in 5 minutes at the given rate of flow of water.
We can write that the volume of the cylindrical pipe that we are considering is by using the information given in the hint as follows
\[\begin{align}
 & \Rightarrow \text{Volume} =\left( \text{area of cross-section} \right)\times \text{height} \\
 & \left[ \text{Volume of cylinder}=\left( \text{area of cross-section} \right)\times \text{height}\right] \\
 & \Rightarrow Volume=10.4\times {{10}^{-4}}\times 15 \\
 & \Rightarrow \text{Volume(per sec )}=153\times {{10}^{-4}}=0.153\ {{m}^{3}} \\
\end{align}\]
 Now, as it is given that the water fills 60% of the pipe always, so the volume of water that comes out of the pipe per sec is as follows
\[\begin{align}
  & \Rightarrow \text{Volume of water(per sec )}=60\%\ of\ Volume(per sec )=153\times {{10}^{-4}}=0.153\ {{m}^{3}} \\
 & \Rightarrow \text{Volume of water(per sec )}=60\%\ of\ 0.153\ {{m}^{3}} \\
 & \Rightarrow \text{Volume of water(per sec )}=\left[ \dfrac{60}{100}\ \times 0.153\ \right]{{m}^{3}} \\
 & \Rightarrow \text{Volume of water(per sec )}=\left[ \dfrac{60}{100}\ \times 0.153\ \right]{{m}^{3}}=0.0918\ {{m}^{3}} \\
\end{align}\]
   As mentioned in the question, we have to find the volume of water that comes out of the pipe in 5 minutes, so for finding that we can write the following
\[\begin{align}
  & \Rightarrow \text{Volume of water (per sec )}=0.0918\ {{m}^{3}} \\
 & \Rightarrow \text{Volume of water(per min)}=0.0918\times 60\ {{m}^{3}}=0.0918\times 60\ {{m}^{3}}=5.508\ {{m}^{3}} \\
 & \Rightarrow \text{Volume of water(in 5 min )}=0.0918\times 60\ {{m}^{3}}=5.508\times 5\ {{m}^{3}}=27.54\ {{m}^{3}} \\
\end{align}\]
Hence, the volume of water that comes out of the pipe in 5 minutes is \[27.54\ {{m}^{3}}\] .
Now, as we know that \[1\ {{m}^{3}}=1000\ l\] , so, we can find that \[27.54\ {{m}^{3}}\] is
\[\begin{align}
  & \left( 1\ {{m}^{3}}=1000\ l \right) \\
 & \Rightarrow 27.54\ {{m}^{3}}=\left( 27.54\times 1000 \right)\ l=27540\ l \\
\end{align}\]

Note:-Another way of understanding the situation more clearly is making a diagram of the volume of the pipe per sec which is as follows

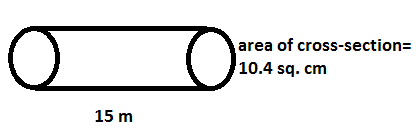
Now, we can imagine that this pipe is 60% full of water all the time. So, we can find the volume of water coming out of it per sec by taking 60% of the volume of the above mentioned pipe.
And then, we can follow the same procedure as done in the solution.