Question

The area of a circle is equal to the area of a rectangle with sides \[112\] m and $88$ m respectively. Find the circumference of the circle.

Answer 1

Hint: First find the area of the rectangle with the use of given sides and then use the given condition that the area of the circle is equal to the area of the rectangle, to find the radius of the circle. Use this obtained radius to find the circumference of the circle.

Complete step-by-step answer:
We have given that the area of the circle is equal to the area of the rectangle with sides\[112\] m and $88$ m respectively.
We have to find the circumference of the circle.

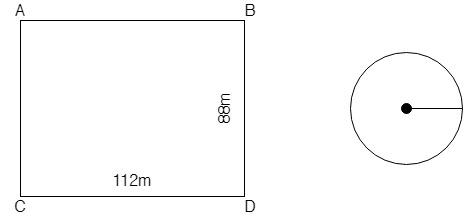
First we find the area of the rectangle. The data given about rectangle:
Length of the rectangle $ = 112$ m
Width of the rectangle $ = 88$ m
Then the area of the rectangle is given as:
Area of rectangle$ = {\text{length}} \times {\text{width}}$
Substitute length as $112$ and width as $88$ into the formula:
Area of rectangle $ = 112 \times 88$
Area of rectangle $ = 9856{\text{ }}{m^2}$
So, the obtained area of the rectangle is$9856{\text{ }}{m^2}$.
Then we take the area of the rectangle equal to the area of the circle.
Area of circle $ = $ Area of rectangle
Substitute the area of the rectangle into the equation.
Area of circle$ = 9856{\text{ }}{m^2}$
We know that the area of the circle is given as:
Area of circle$ = \pi {r^2}$
Put the area as $9856{\text{ }}{m^2}$ in the above equation:
$9856 = \pi {r^2}$
Substitute $\pi = \dfrac{{22}}{7}$ in the above equation:
$\Rightarrow$ $9856 = \left( {\dfrac{{22}}{7}} \right){r^2}$
$\Rightarrow$ $9856 \times \dfrac{7}{{22}} = {r^2}$
$\Rightarrow$ ${r^2} = 448 \times 7$
$\Rightarrow$ ${r^2} = 3136$
$\Rightarrow$ $r = \sqrt {3136} $
$\Rightarrow$ $r = 56{\text{ m}}$
Hence, we get that the radius of the circle is 56 m.
As we have to find the circumference of the circle, we will use the formula for the circumference of the circle.
Circumference of the circle$ = 2\pi r$
Substitute radius $\left( {r = 56} \right)$ and $\pi = \dfrac{{22}}{7}$into the above equation:
Circumference of the circle$ = 2\left( {\dfrac{{22}}{7}} \right)\left( {56} \right)$
Circumference of the circle$ = 2 \times 22 \times 8$
Circumference of the circle$ = 352{\text{ m}}$
Hence, the circumference of the circle is $352{\text{ m}}$.

Note: Always remember that the unit of area is always a square unit and the unit of any length like length and width of the rectangle are simply the length so we use SI units for them, even circumference of the circle is also a length. But for the volume, we always use a cubic unit.