Question

The area bounded by the circles ${x^2} + {y^2} = 1$ and ${x^2} + {y^2} = 4$ , and the pair of lines $\sqrt 3 ({x^2} + {y^2}) = 4xy$ in the first quadrant is equal to:
$
  (1){\text{ }}\dfrac{\pi }{2} \\
  (2){\text{ }}5\dfrac{\pi }{2} \\
  (3){\text{ }}3\pi \\
  (4){\text{ }}\dfrac{\pi }{4} \\
 $

Answer 1

Hint: Here we have given two equations of circle and a pair of straight lines is given so first of all we have to find individual equations of straight line and then draw a diagram of all the curves given and then shade the region in first quadrant which is formed by all four equations. And now we have to just find the area of that shaded diagram.

Complete step by step answer:
Given- Circle 1: ${x^2} + {y^2} = 1$ and Circle 2: ${x^2} + {y^2} = 4$
Pair of lines: $\sqrt 3 ({x^2} + {y^2}) = 4xy$
Find the individual equations of the straight lines. We have
$\sqrt 3 {x^2} - 4xy + \sqrt 3 {y^2} = 0$
Factorizing,$\sqrt 3 {x^2} - 3xy - xy + \sqrt 3 {y^2} = 0$
Simplifying,$(x - \sqrt 3 y)(\sqrt 3 x - y)$
Line 1: $x - \sqrt 3 y = 0$ Line 2: $\sqrt 3 x - y = 0$

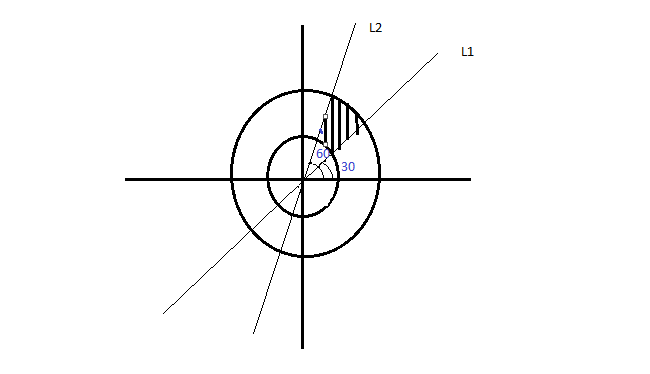
We need to find the shaded area. For this, we will use the sector formula.
When area of only a sector of a circle covering $\theta $ angle is to be found:
$\dfrac{\theta }{{2\pi }} \times \pi {r^2}$
Here, since we have to find the area of the region between two circles:$\dfrac{\theta }{{2\pi }} \times \pi [r_2^2 - r_1^2]$
The angle $\theta $ here is (60 - 30 = 30) i.e. $\dfrac{\pi }{6}$
${r_2} = 2{\text{ , }}{{\text{r}}_1} = 1$
On solving, we get
Area = $\dfrac{\pi }{4}$ .

So, the correct answer is “Option 4”.

Note: Whenever we get this type of question the key concept of solving is we should have knowledge on how to find individual equations of straight line when the equation of pair of straight lines is given. The formula of area of sector should be remembered. Area of sector = $\dfrac{\theta }{{2\pi }} \times \pi {r^2}$.