Question

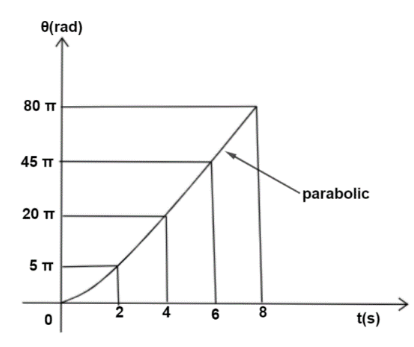
The angular displacement $\left( \theta \right)$ of the blades of a ceiling fan, when the fan is switched on at $t = 0$, is shown in figure. The average angular velocity of the fan blades during the first $8$ seconds will be

A. $40\pi {\text{ rad/s}}$
B. $20\pi {\text{ rad/s}}$
C. $10\pi {\text{ rad/s}}$
D. $5\pi {\text{ rad/s}}$

Answer 1

Hint: To solve this question the student should know what angular displacement is. Its definition, formulas and unit of angular displacement. One has to clearly observe the given graph and data to solve the question. And should know about average angular displacement.

Complete step by step answer:
The motion of the body along a circular path is known as the rotational motion and angular displacement can be defined as the shortest angle between the initial and the final position for an object in a circular motion around a fixed point is known as the angular displacement.It is a vector quantity.

The unit of angular displacement is radian or degrees.
Formula for angular displacement
$\theta = \dfrac{s}{r}$
Where, $\theta $ is angular displacement, $s$ is distance covered and $r$ is the radius of curvature.
\[{\omega _{avg}} = \dfrac{{{\text{angular displacement}}}}{{{\text{total time taken}}}}\]
\[{\omega _{avg}} = \dfrac{{\Delta \theta }}{{\Delta t}}\]
Substituting the given values,
\[ \Rightarrow {\omega _{avg}} = \dfrac{{80\pi }}{8}\]
\[ \therefore {\omega _{avg}} = 10\pi \]

Therefore, the correct answer is option C.

Note: With these types of questions, one should not forget to write the SI along with the answer. Actually angular displacement has no unit but just to avoid confusion Here the SI unit of angular displacement is given by radian or degree. And Angular velocity: The angular velocity is the rate at which displacement is changing with respect to the time in circular motion.