
The angles of depression of top and bottom of a building $50\,m$ high as observed from
top of a tower are ${{30}^{o}}$ and ${{60}^{o}}$, respectively. Find the height of the tower and also
the horizontal distance between the building and the tower.
Answer
606.9k+ views
Hint: The given question is related to heights and distance. Try to recall Try to recall the formulae
related to trigonometric ratios and values of trigonometric functions for standard angles.
The following formulae will be used to solve the given problem:
(a) $\tan \theta =\dfrac{opposite\,side}{adjacent\,side}$
(b) $\tan \left( {{30}^{o}} \right)=\dfrac{1}{\sqrt{3}}$
(c) $\tan \left( {{60}^{o}} \right)=\sqrt{3}$
Complete step by step solution:
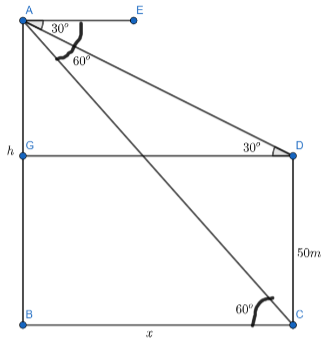
Now, considering the information given in the question, we can draw the following figure for better visualization of the problem:
Let $AB$ be the tower of height $h\,$meter and $CD$ be the building of height $50\,m$ . Let $x$
meter be the horizontal distance between the building and the tower. We will consider a point $G$
on the tower $AB$ which is at the same level as the top of the building $CD$ . So, \[BG=50\,m\] and
$AG=\left( h-50 \right)\,m$ . Also, $GD=x$ meter . In the question, it is given that the angle of
depression of top and bottom of the building as seen from the top of the tower are ${{30}^{o}}$ and
${{60}^{o}}$ respectively. So, , $\measuredangle EAC={{60}^{o}}$ and $\measuredangle
EAD={{30}^{o}}$.
Now, $AE$ and $BC$ are horizontal lines. So, they are parallel to each other. So, $\measuredangle
EAC$ and $\measuredangle ACB$ are alternate interior angles. So, they will be equal. Also,
$\measuredangle EAD$ and $\measuredangle ADG$ are also alternate interior angles. So, they will
also be equal. So, \[\measuredangle ACB=\measuredangle EAC={{60}^{o}}\] and \[\measuredangle
ADG=\measuredangle EAD={{30}^{o}}\].
Now, we will consider $\Delta ADG$.
In $\Delta ADG$ ,
$\tan \left( {{30}^{0}} \right)=\dfrac{h-50}{x}$
$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{h-50}{x}$
$\Rightarrow x=\sqrt{3}\left( h-50 \right)......(i)$
Now, we will consider $\Delta ACB$ .
In $\Delta ACB$,
$\tan \left( {{60}^{o}} \right)=\dfrac{h}{x}$
$\Rightarrow \sqrt{3}=\dfrac{h}{x}$
$\Rightarrow x=\dfrac{h}{\sqrt{3}}......(ii)$
Now, the distance between the tower and the building is the same in both cases. So, $(i)=(ii)$ .
$\Rightarrow \sqrt{3}\left( h-50 \right)=\dfrac{h}{\sqrt{3}}$
On cross-multiplying, we get:
$3\left( h-50 \right)=h$
$\Rightarrow 3h-150=h$
$\Rightarrow 2h=150$
$\Rightarrow h=75\,m$
Substituting $h=75$ in equation $(ii)$ , we get:
$x=\dfrac{75}{\sqrt{3}}\,m$
Hence, the height of the tower is $75\,m$ and the distance between the building and tower is equal
to $\dfrac{75}{\sqrt{3}}\,m$.
Note: Students are generally confused between the values of $\tan \left( {{30}^{o}} \right)$ and $\tan \left( {{60}^{o}} \right)$. $\tan \left( {{30}^{o}} \right)=\dfrac{1}{\sqrt{3}}$ and $\tan \left({{60}^{o}} \right)=\sqrt{3}$. These values should be remembered as they are used in various problems of heights and distances.
related to trigonometric ratios and values of trigonometric functions for standard angles.
The following formulae will be used to solve the given problem:
(a) $\tan \theta =\dfrac{opposite\,side}{adjacent\,side}$
(b) $\tan \left( {{30}^{o}} \right)=\dfrac{1}{\sqrt{3}}$
(c) $\tan \left( {{60}^{o}} \right)=\sqrt{3}$
Complete step by step solution:

Now, considering the information given in the question, we can draw the following figure for better visualization of the problem:
Let $AB$ be the tower of height $h\,$meter and $CD$ be the building of height $50\,m$ . Let $x$
meter be the horizontal distance between the building and the tower. We will consider a point $G$
on the tower $AB$ which is at the same level as the top of the building $CD$ . So, \[BG=50\,m\] and
$AG=\left( h-50 \right)\,m$ . Also, $GD=x$ meter . In the question, it is given that the angle of
depression of top and bottom of the building as seen from the top of the tower are ${{30}^{o}}$ and
${{60}^{o}}$ respectively. So, , $\measuredangle EAC={{60}^{o}}$ and $\measuredangle
EAD={{30}^{o}}$.
Now, $AE$ and $BC$ are horizontal lines. So, they are parallel to each other. So, $\measuredangle
EAC$ and $\measuredangle ACB$ are alternate interior angles. So, they will be equal. Also,
$\measuredangle EAD$ and $\measuredangle ADG$ are also alternate interior angles. So, they will
also be equal. So, \[\measuredangle ACB=\measuredangle EAC={{60}^{o}}\] and \[\measuredangle
ADG=\measuredangle EAD={{30}^{o}}\].
Now, we will consider $\Delta ADG$.
In $\Delta ADG$ ,
$\tan \left( {{30}^{0}} \right)=\dfrac{h-50}{x}$
$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{h-50}{x}$
$\Rightarrow x=\sqrt{3}\left( h-50 \right)......(i)$
Now, we will consider $\Delta ACB$ .
In $\Delta ACB$,
$\tan \left( {{60}^{o}} \right)=\dfrac{h}{x}$
$\Rightarrow \sqrt{3}=\dfrac{h}{x}$
$\Rightarrow x=\dfrac{h}{\sqrt{3}}......(ii)$
Now, the distance between the tower and the building is the same in both cases. So, $(i)=(ii)$ .
$\Rightarrow \sqrt{3}\left( h-50 \right)=\dfrac{h}{\sqrt{3}}$
On cross-multiplying, we get:
$3\left( h-50 \right)=h$
$\Rightarrow 3h-150=h$
$\Rightarrow 2h=150$
$\Rightarrow h=75\,m$
Substituting $h=75$ in equation $(ii)$ , we get:
$x=\dfrac{75}{\sqrt{3}}\,m$
Hence, the height of the tower is $75\,m$ and the distance between the building and tower is equal
to $\dfrac{75}{\sqrt{3}}\,m$.
Note: Students are generally confused between the values of $\tan \left( {{30}^{o}} \right)$ and $\tan \left( {{60}^{o}} \right)$. $\tan \left( {{30}^{o}} \right)=\dfrac{1}{\sqrt{3}}$ and $\tan \left({{60}^{o}} \right)=\sqrt{3}$. These values should be remembered as they are used in various problems of heights and distances.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




