Question

The angles of a triangle are in A.P and the least angle is \[{{30}^{o}}\]. What is the greatest angle (in radian)?
(a) \[\dfrac{\pi }{2}\]
(b) \[\dfrac{\pi }{3}\]
(c) \[\dfrac{\pi }{4}\]
(d) \[\pi \]

Answer 1

Hint: First of all, we know that the general terms of A.P are like a, a + d, a + 2d…..So, first, assume the angles of the triangle as \[{{30}^{o}},\text{ }{{30}^{o}}+d,\text{ }{{30}^{o}}+2d\]. Equate the sum of these angles to \[{{180}^{o}}\] and get the value of d. Use the value of d to find the greatest angle.

Complete step-by-step answer:

We are given that the angles of the triangle are in A.P and the least angle is \[{{30}^{o}}\]. We have to find the greatest angle (in radian). Let us first see what arithmetic progression is. Arithmetic Progression (A.P) is a sequence of numbers so that the difference of any two successive numbers is a constant value. For example, the series of natural numbers: 1, 2, 3, 4, 5, 6…. are in A.P with the first term as 1 and common difference as 1. Also, the nth term of A.P is \[{{a}_{n}}=a+\left( n-1 \right)d\] where ‘a’ is the first term, and ‘d’ is the common difference.

So, we know that the general terms of any arithmetic progression (A.P) are in the form a, a + d, a + 2d, a + 3d…….Here, ‘a’ is the first term and ‘d’ is the common difference of A.P. We are given that the least angle of the triangle is \[{{30}^{o}}\] and all three angles are in A.P. So, let us assume the other two angles as \[{{30}^{o}}+d\] and \[{{30}^{o}}+2d\]. So, we get 3 angles of the triangle as, \[{{30}^{o}},\text{ }{{30}^{o}}+d,\text{ }{{30}^{o}}+2d\]

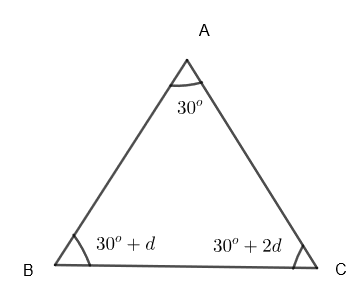
Also, we know that in any triangle, the sum of each of the angles is \[{{180}^{o}}\]. So, we get, \[\angle A+\angle B+\angle C={{180}^{o}}\]

By substituting the values of \[\angle A,\text{ }\angle B\text{ and }\angle C\], we get, \[{{90}^{o}}+3d={{180}^{o}}\]
\[\Rightarrow 3d={{180}^{o}}-{{90}^{o}}\]
\[3d={{90}^{o}}\]
By dividing 3 on both the sides, we get, \[d=\dfrac{{{90}^{0}}}{3}={{30}^{o}}\]
So, we get 3 angles of the triangle as,
\[\begin{align}
  & \angle A={{30}^{o}} \\
 & \angle B={{30}^{o}}+d={{30}^{o}}+{{30}^{o}}={{60}^{o}} \\
 & \angle C={{30}^{o}}+2d={{30}^{o}}+2\left( {{30}^{o}} \right)={{90}^{o}} \\
\end{align}\]
So, we get the greatest angle as \[{{90}^{o}}\]. To get this angle in radian, we will multiply it with \[\dfrac{\pi }{{{180}^{o}}}\]. So, we get,
Greatest Angle \[={{90}^{o}}\times \dfrac{\pi }{{{180}^{o}}}=\dfrac{\pi }{2}\]

Hence, option (a) is the right answer.

Note: In this question, students often take three angles in the arithmetic progression (A.P) as \[\left( {{30}^{o}}-d \right),{{30}^{o}},\left( {{30}^{o}}+d \right)\] but this is wrong because it is given in the question that the least angle is \[{{30}^{o}}\]. So we must start writing the terms with \[{{30}^{o}}\]. Also, the sum of all the angles of the triangle is \[{{180}^{o}}\], but in the above case, as we can see that \[\left( {{30}^{o}}-d \right)+\left( {{30}^{o}} \right)+\left( {{30}^{o}}+d \right)={{90}^{o}}\] which is incorrect. So, this point must be taken care of and take the 3 angles in A.P as \[\left( {{30}^{o}} \right),\left( {{30}^{o}}+d \right)\text{ and }\left( {{30}^{o}}+2d \right)\].