Question

The angle of elevation of the top of the hill at the foot of a tower is ${{60}^{0}}$ and the angle of elevation of the top of the tower from the foot of the hill is ${{30}^{0}}$ . If the tower is 50 m high, what is the height of the hill?

Answer 1

Hint: For solving this problem first we will draw the geometrical figure as per the given data. After that, we will use the basic formula of trigonometry $\tan \theta =\dfrac{\left( \text{length of the perpendicular} \right)}{\left( \text{length of the base} \right)}$ . Then, we will solve correctly to get the correct answer.
Complete step-by-step answer:
Given:
It is given that, angle of elevation of the top of the hill at the foot of a tower is ${{60}^{0}}$ and the angle of elevation of the top of the tower from the foot of the hill is ${{30}^{0}}$ . Moreover, it is given that the height of the tower is 50 m and we have to find the height of the hill.
Now, first, we will draw a geometrical figure as per the given data. For more clarity look at the figure given below:

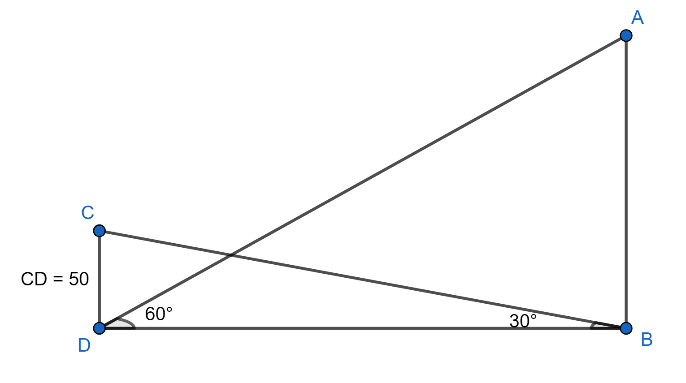
In the above figure, AB represents the height of the hill, CD represents the 50 m height of the tower. Moreover, as it is given that angle of elevation of the top of the hill at the foot of a tower is $\angle BDA={{60}^{0}}$ an angle of elevation of the top of the tower from the foot of the hill is $\angle DBC={{30}^{0}}$ .
Now, we consider $\Delta CDB$ in which $\angle CDB={{90}^{0}}$ , $CD=50$ is the length of the perpendicular, DB is the length of the base and $\angle DBC={{30}^{0}}$ . Then,
$\begin{align}
  & \tan \left( \angle DBC \right)=\dfrac{\left( \text{length of the perpendicular} \right)}{\left( \text{length of the base} \right)} \\
 & \Rightarrow \tan {{30}^{0}}=\dfrac{CD}{DB} \\
 & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{50}{DB} \\
 & \Rightarrow DB=50\sqrt{3}.........................\left( 1 \right) \\
\end{align}$
Now, we consider $\Delta ADB$ in which $\angle DBA={{90}^{0}}$ , AB is the length of the perpendicular, DB is the length of the base and $\angle BDA={{60}^{0}}$ . Then,
$\begin{align}
  & \tan \left( \angle BDA \right)=\dfrac{\left( \text{length of the perpendicular} \right)}{\left( \text{length of the base} \right)} \\
 & \Rightarrow \tan {{60}^{0}}=\dfrac{AB}{DB} \\
 & \Rightarrow \sqrt{3}=\dfrac{AB}{DB} \\
 & \Rightarrow AB=DB\sqrt{3} \\
\end{align}$
Now, put $DB=50\sqrt{3}$ from equation (1) into the above equation. Then,
$\begin{align}
  & AB=DB\sqrt{3} \\
 & \Rightarrow AB=50\sqrt{3}\times \sqrt{3} \\
 & \Rightarrow AB=150 \\
\end{align}$
Now, from the above result, we conclude that the height of the hill will be 150 metres.

Note: Here, the student should first try to understand what is asked in the problem. After that, we should try to draw the geometrical figure as per the given data and proceed stepwise. Moreover, we should apply the basic formula of trigonometry properly without any error and avoid calculation mistakes while solving to get the correct answer. We can use cot as well instead of tan.