Question

The angle of elevation of the top of a T.V. tower from three points A, B, C in a straight line in the horizontal plane through the foot of the tower are $\alpha ,2\alpha ,3\alpha $ respectively. If$AB=a$ , the height of the tower is

A) $a\tan \alpha$
B) $a\sin \beta $
C) $a\sin 2\alpha $
D) $a\sin 3\alpha $

Answer 1

Hint:
Here we have to calculate the height of the T.V. tower. For that, we will first draw a line and will mark three points A, B and C on that line. Then we will mark a point in front of that line considering that point as the top point of the tower and we will join all the points one by one to that top point. We will assume the value of height of the tower to be any variable and then will use a tangent formula in the triangle that we get after joining points. From there we will get the value of the height of the T.V. tower.

Complete step by step solution:
We will draw a straight line and we will mark the point A, B, C on the line.

Now, we will mark the point D assuming this to be the top of the tower. We will join all the points on the line with the point D and then we will draw a perpendicular line from the point D to the line and mark that point as E.

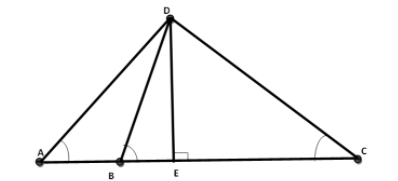
According to the question, $\angle DAE=\alpha ,\angle DBE=2\alpha \And \angle DCE=3\alpha $. Also, $AB=a$
Let the height of the tower be H i.e. $DE=H$ and let $BE=x$ and CE = Y.
We will label the figure and redraw it again.

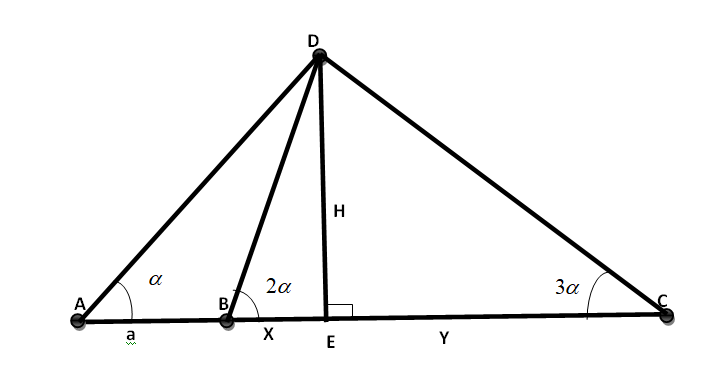
Now, we will take triangle ADE
Here
$\angle DAE = \alpha$
We know, $\tan \theta =\dfrac{perpendicular}{base}$
Here the angle is
Therefore,
$\Rightarrow \tan \alpha =\dfrac{H}{a+X}$……………….$(1)$
Now, we will take triangle BDE
Here
$\angle DBE=2\alpha $
We know, $\tan \theta =\dfrac{perpendicular}{base}$
Here the angle is
Therefore,
$\Rightarrow \tan 2\alpha =\dfrac{H}{X}$……………….$(2)$
We can write equation 2 as;
$\Rightarrow H=Y\tan 2\alpha $
Putting value of H in equation 1, we get
$\Rightarrow \tan \alpha =\dfrac{X\tan 2\alpha }{a+X}$
On cross multiplying the terms, we get
$\Rightarrow \left( a+X \right)\tan \alpha =X\tan 2\alpha $…………..$(3)$
We know the formula:-
$\Rightarrow \tan 2\alpha =\dfrac{2\tan \alpha }{1-{{\tan }^{2}}\alpha }$
Now, putting value of in equation 3, we get
$\Rightarrow \left( a+X \right)\tan \alpha =X\dfrac{2\tan \alpha }{1-{{\tan }^{2}}\alpha }$
Cancelling the terms and cross multiplying the terms, we get
$\Rightarrow \left( a+X \right)\left( 1-{{\tan }^{2}}\alpha \right)=2X$
Using distributive property of multiplication, we get
$\Rightarrow a-a{{\tan }^{2}}\alpha +X-X{{\tan }^{2}}\alpha =2X$
On further simplification, we get
$\begin{align}
  &\Rightarrow a\left( 1-{{\tan }^{2}}\alpha \right)=X\left( 1-{{\tan }^{2}}\alpha \right) \\ \Rightarrow
 &\Rightarrow X=a\dfrac{\left( 1-{{\tan }^{2}}\alpha \right)}{\left( 1-{{\tan }^{2}}\alpha \right)} \\
\end{align}$
Putting value of X in equation 1, we get
$\Rightarrow \tan \alpha =\dfrac{H}{a+a\dfrac{\left( 1-{{\tan }^{2}}\alpha \right)}{\left( 1-{{\tan }^{2}}\alpha \right)}}$
On further simplification, we get
$\Rightarrow H=\dfrac{2a\tan \alpha }{{{\sec }^{2}}\alpha }$
We will break the terms now.
$\Rightarrow H=\dfrac{2a\dfrac{\sin \alpha }{\cos \alpha }}{\dfrac{1}{{{\sec }^{2}}\alpha }}$
On simplifying it further, we get
$\Rightarrow H=2a\sin \alpha \cos \alpha $
We know, $2\sin \alpha \cos \alpha =\sin 2\alpha $
Therefore,
$\Rightarrow H=a\sin 2\alpha $

Therefore, the height of the tower is $a\sin 2\alpha $
So the correct option is C.

Note:
Since we have applied a cross multiplication method here, let’s understand it deeply.
A cross multiplication method is defined as a method in which we multiply the denominator of the first fraction with the numerator of the second fraction and we multiply the denominator of the second fraction with the numerator of the first fraction.
A cross multiplication method is also used in the addition and subtraction of unlike fractions.