Question

The angle of elevation of the top of a tower at a distance 30 m from its foot on a horizontal plane is found to be . Find the height of the tower.
A. 17.3 m
B. 57.96 m
c. 17.8 m
D. 173 m

Answer 1

 Hint: Here, we will be using the formula of trigonometry to find the height of the tower.

Complete step-by-step answer:
Given:
The angle of elevation of the top of a tower at a distance 30 m from its foot on a horizontal plane is found to be $ 30^{\circ} $
Draw the figure:

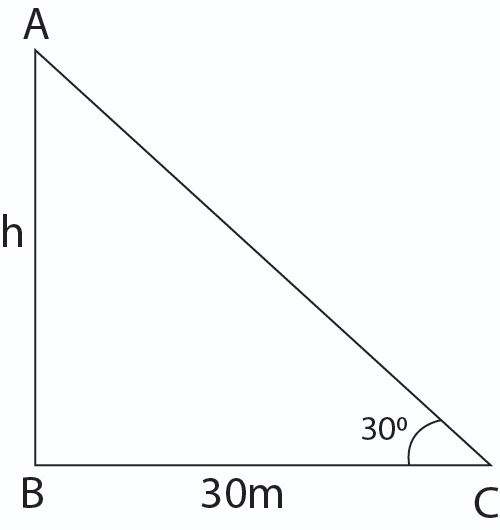
$tan \theta $ is given by $\dfrac{P}{B}$ where P is the perpendicular of the right angled triangle and B is the base of the right angled triangle.
The base of the triangle is given as 30 m.
The perpendicular of the triangle is assumed as h and we need to find the value of h.
The angle of the triangle is given as$ 30^{\circ} $.
Use the trigonometric formula to find h.
$ tan 30^{\circ} = \dfrac{h}{30}$
The value of $ tan 30^{\circ} $is $\dfrac{1}{\sqrt{3}}$
Put the value of $ tan 30^{\circ} $ in the equation.
$\dfrac{1}{\sqrt{3}}=\dfrac{h}{30}$
Cross multiply and find the value of h.
$h=\dfrac{30}{\sqrt{3}}$
Simplifying the value, h=17.3 m

Note: In these types of problems first use the known values.