Question

The angle of elevation of a stationary cloud from a point 2500 m above a lake is ${{15}^{\circ }}$ and the angle of depression of its reflection in lake is ${{45}^{\circ }}$. What is the height of the cloud above the lake level? (Use $\tan {{15}^{\circ }}=0.268$)

Answer 1

Hint: Assume that the height of the cloud above the lake level is ‘h’. Draw a rough diagram of the given conditions and then use the formula $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$ in the different right angle triangles and substitute the given values to get the height.

Complete step by step answer:

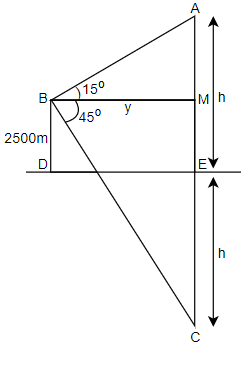
According to the above figure:
Let A be the stationary cloud and the observer is at point B which is 2500 m above the lake level. Let the reflection of the cloud below the lake level is at point C. Point D and E are at lake level.
We have assumed the height of the cloud above the lake level as ‘h’. Therefore, AE = h. Also, assume that the distance BM is ‘y’.
Now, in right angle triangle ABM,
$\angle ABM={{15}^{\circ }}$
We know that, $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$. Therefore,
$\tan {{15}^{\circ }}=\dfrac{AM}{BM}$
Since, BD = ME = 2500 m, because they are opposite sides of the rectangle BDEM. Therefore,
AM = AE – EM = h – 2500.
$\begin{align}
  & \Rightarrow \tan {{15}^{\circ }}=\dfrac{AM}{BM} \\
 & \Rightarrow \tan {{15}^{\circ }}=\dfrac{h-2500}{y} \\
 & \Rightarrow y=\dfrac{h-2500}{\tan {{15}^{\circ }}}.......................(i) \\
\end{align}$
Now, in right angle triangle BMC,
\[\angle CBM={{45}^{\circ }}\]
We know that, $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$. Therefore,
$\tan {{45}^{\circ }}=\dfrac{CM}{BM}$
We know that, from the laws of angle of reflection we have, the distance of the object and its image formed by the plane mirror are equal. Therefore, considering the lake as the plane mirror, we have,
AE = CE = h.
CM = CE + ME = h + 2500
\[\begin{align}
  & \Rightarrow \tan {{45}^{\circ }}=\dfrac{h+2500}{y} \\
 & \Rightarrow y=\dfrac{h+2500}{\tan {{45}^{\circ }}}.......................(ii) \\
\end{align}\]
From equations (i) and (ii), we get,
$\dfrac{h-2500}{\tan {{15}^{\circ }}}=\dfrac{h+2500}{\tan {{45}^{\circ }}}$
Substituting $\tan {{45}^{\circ }}=1$, we get,
$\dfrac{h-2500}{\tan {{15}^{\circ }}}=\dfrac{h+2500}{1}$
By cross multiplication, we get,
$\begin{align}
  & h-2500=h\tan {{15}^{\circ }}+2500\tan {{15}^{\circ }} \\
 & \Rightarrow h-h\tan {{15}^{\circ }}=2500\tan {{15}^{\circ }}+2500 \\
 & \Rightarrow h(1-\tan {{15}^{\circ }})=2500(\tan {{15}^{\circ }}+1) \\
 & \Rightarrow h=\dfrac{2500(\tan {{15}^{\circ }}+1)}{(1-\tan {{15}^{\circ }})} \\
\end{align}$
Substituting the value, $\tan {{15}^{\circ }}=0.268$, we get,
$\begin{align}
  & h=\dfrac{2500(0.268+1)}{(1-0.268)} \\
 & \Rightarrow h=\dfrac{2500\times 1.268}{0.732} \\
 & \Rightarrow h=4330.60 \\
\end{align}$

So, the height of the cloud from the lake level is 4330.60 m.

Note: One may get confused in removing the unknown variables. Therefore, remember that we have to find the value of variable ‘h’ and we have to remove all other variables. We have used the tangent of the given angle because we have to find the height and we have a common base in two right angle triangles that can be easily cancelled.