Question

The angle of elevation of a jet plane from a point on the ground is ${{60}^{\circ }}$. After a flight of 30 seconds, the angle of elevation changes to ${{30}^{\circ }}$. If the jet plane is flying at a constant height of $3600\sqrt{3}$ m, find the speed of the jet plane.

Answer 1

Hint: Assume a variable s which will represent the speed of the jet plane in m/s. According to the information given in the question, we can make the figure of the whole situation given in the question. The distance is given by multiplying the speed with the time. Also, from trigonometry, the tan of any angle is given by the ratio of height and the base of the right triangle. Using this, we can solve this question.

Complete step-by-step answer:
Before proceeding with the question, we must know all the formulas that will be required to solve this question.
The distance is given by the product of speed and the time . . . . . . . . . (1)
From trigonometry, the tan of an angle is equal to the ratio of perpendicular height and the base of the triangle . . . . . . . . . . . . (2)
Let us draw the figure according to the information given in the question.

In this question, it is given that the angle of elevation of a jet plane at a point A from a point C on the ground is ${{60}^{\circ }}$. After a flight of 30 seconds, the plane reaches point B and the angle of elevation from point C changes to ${{30}^{\circ }}$. Also, it is given that the height of the plane is constant and is equal to $3600\sqrt{3}$ m. So, we can say that AD = BE = $3600\sqrt{3}$.

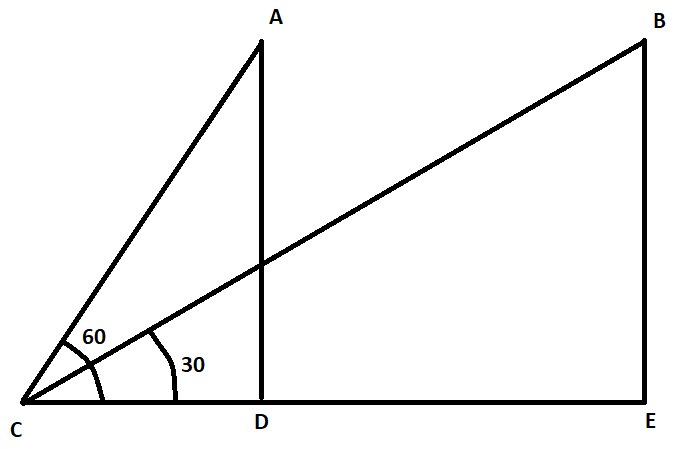
Let us assume that the plane is moving at a speed of s m/s. Since the time of flight is 30 s, from formula (1), the distance AB = DE = 30s.
In triangle ACD, using formula (2) at angle C, we get,
$\begin{align}
  & \tan 60=\dfrac{AD}{CD} \\
 & \Rightarrow CD=\dfrac{AD}{\tan 60} \\
\end{align}$

Substituting AD = $3600\sqrt{3}$ and $\tan 60=\sqrt{3}$, we get,
$\begin{align}
  & CD=\dfrac{3600\sqrt{3}}{\sqrt{3}} \\
 & \Rightarrow CD=3600 \\
\end{align}$
In triangle BCE, using formula (2) at angle C, we get,
$\begin{align}
  & \tan 30=\dfrac{BE}{CE} \\
 & \Rightarrow CE=\dfrac{BE}{\tan 30} \\
 & \Rightarrow CD+DE=\dfrac{BE}{\tan 30} \\
\end{align}$

Substituting BE = $3600\sqrt{3}$ and $\tan 30=\dfrac{1}{\sqrt{3}}$, CD = 3600 and DE = 30 s, we get,
$\begin{align}
  & 3600+30s=\dfrac{3600\sqrt{3}}{\dfrac{1}{\sqrt{3}}} \\
 & \Rightarrow 30s=\left( 3600\times \sqrt{3}\times \sqrt{3} \right)-3600 \\
 & \Rightarrow 30s=3600\left( 3-1 \right) \\
 & \Rightarrow s=120\left( 2 \right) \\
 & \Rightarrow s=240m/s \\
\end{align}$
Hence, the speed of the jet plane is 240 m/s.

Note: This question is an easy question which can be done if one draws the figure correctly. There is a possibility that one may commit a mistake while drawing the figure. It is possible that one may consider the initial angle of elevation as $\angle CAD$ instead of $\angle ACD$ which will lead us to an incorrect answer.