Question

The angle of depression of a car parked on the road from the top of a \[150\] meter high tower is \[{30^ \circ }\]. The distance of the car from the tower (in meters) is
A. \[50\sqrt 3 \]
B. \[150\sqrt 3 \]
C. \[150\sqrt 2 \]
D. \[75\]

Answer 1

Hint: Here we draw a diagram where we take one point where the car is parked and one point as top of the building, and using the angle of depression given in the question we apply, we apply tan of angle which will give us perpendicular divided by base in a right triangle.
* Angle of depression is the angle formed between the horizontal line and line of sight. Generally an observer needs to be at a higher position than the object to have an angle of depression.

               

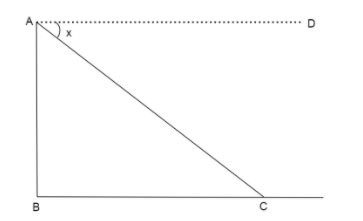
If C is an object placed at ground level and A is the point where the observer is placed then the horizontal line is AD and the line of sight is AC. So, the angle of depression formed is x.

Complete step-by-step answer:
We draw a diagram depicting the situation where a have car parked on the road at point C and the observer is at the top of \[150\] meter high building at point A. Then the building forms a right angle with the ground, and angle of depression is given to be \[{30^ \circ }\].
We draw the horizontal line AD which is parallel to the ground and is depicted as a dotted line in the figure.

               

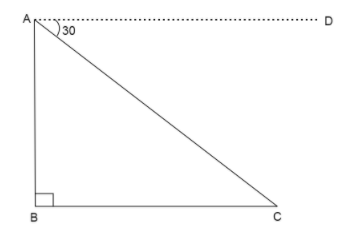
Looking at the figure, we have lines \[AD\parallel BC\] because the horizontal line is parallel to the ground.
So, let us take a transversal \[AC\] which cuts the parallel lines \[AD\parallel BC\].
Then the set of alternate interior angles are \[\angle BCA,\angle CAD\].
Now we know when the parallel lines are cut by a transversal then the set of alternate interior angles is equal.
\[ \Rightarrow \angle BCA = \angle CAD = {30^ \circ }\]
Now in \[\vartriangle ABC\], \[\angle B = {90^ \circ }\]
So \[\vartriangle ABC\] is a right angled triangle with BC as base, AC as hypotenuse and AB as the perpendicular.
Now we know that in a right triangle, tan of the angle is given by dividing perpendicular by base.
\[ \Rightarrow \tan \theta = \dfrac{{AB}}{{BC}}\]
Now we know the angle \[\theta = {30^ \circ }\]and the perpendicular \[AB = 150\]
\[ \Rightarrow \tan {30^ \circ } = \dfrac{{150}}{{BC}}\]
We know the value of \[\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}\]
\[ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{150}}{{BC}}\]
Cross multiplying both sides
\[ \Rightarrow BC = 150\sqrt 3 \]
So, the distance of the car from the tower is \[150\sqrt 3 \]meters.

So, the correct answer is “Option B”.

Note: Students many times make the mistake of assuming the angle of depression as the angle formed by line of sight and the height of the line where the observer is placed which is wrong. Also, students many times write their answer without the unit, keep in mind always write the unit along with the answer.