Question

The angle of banking θ for a cyclist taking curve is given by \[\tan \theta = \dfrac{{{v^n}}}{{rg}}\], where symbols ($v$ =speed of the cyclist, $r$ = radius of the curved path, $g$ = acceleration due to gravity) have their usual meanings. Then the value of n is equal to
A. 1
B. 3
C. 2
D. 4

Answer 1

Hint: The appropriate value for n used in the expression \[\tan \theta = \dfrac{{{v^n}}}{{rg}}\] can be calculated with the help of (FBD) free body diagram of the cyclist which is taking turns on the banked road. After that, we apply Newton’s second law to establish the equations of motion for the cyclist along the vertical. Then analyze each component of forces acting on the cyclist separately to get the required value for n.

Complete step by step solution:
Applying Newton’s second law of motion along both the vertical and horizontal axis as:

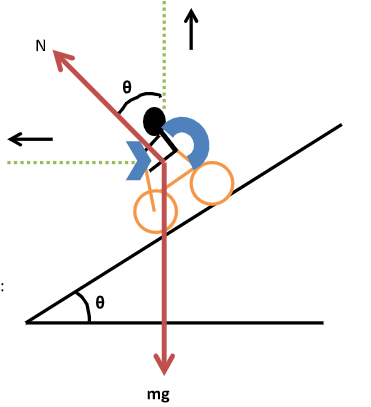
Equation of motion along horizontal direction:
\[N\sin \theta = \dfrac{{m{v^2}}}{r}\]…… (i)
Equation of motion along vertical direction:
\[N\cos \theta = mg\]………. (ii)
Divide equation (ii) by equation (ii), we get
\[\dfrac{{N\sin \theta }}{{N\cos \theta }} = \dfrac{{\dfrac{{m{v^2}}}{r}}}{{mg}}\]
\[ \Rightarrow \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{{{v^2}}}{{rg}}\]
\[\tan \theta = \dfrac{{{v^2}}}{{rg}}\]……………..(iii)
Since we have given that-
\[\tan \theta = \dfrac{{{v^n}}}{{rg}}\]…………(iv)
On comparing both equation (iii) and equation (iv), we get
\[n = 2\]

$\therefore $ The required value of $n=2$. Hence, option (C) is the correct answer.

Note:
In order to tackle these kinds of conceptual questions we should have knowledge of drawing FBD (Free Body Diagram) of a dynamic system and also know how to implement Newton’s second law motion for solving problems on Newton’s law. Banking of roads is developed on turning to avoid the dependence of friction.
From the equation (iii), we can also establish the expression that relates banking angle and radius with speed for a cyclist taking a curve on the banked road as-
\[v = \sqrt {rg\tan \theta } \]
This is actually a speed at which the cyclist does not slide down even the inclined surface is smooth. But there is some limiting value to stay on the same path while taking a turn:
(i) When the speed of the cyclist less than the speed \[\sqrt {rg\tan \theta } \] the cycle will move down while
(ii) When the speed of the cyclist is less than the speed \[\sqrt {rg\tan \theta } \] the cycle will move up to the inclined.