Question

The angle of a prism is A. One of its refracting surfaces is silvered. Light rays falling at an angle of incidence 2A on the first surface returns back through the same path after suffering reflection at the silvered surface. The refractive index μ, of the prism, is :
A. \[2\sin A\]
B. \[2\cos A\]
C. \[\dfrac{1}{2}\cos A\]
D. \[\tan A\]

Answer 1

Hint: Here to find the refractive index of the prism, we can use Snell’s law. It relates the angle of incidence, angle of refraction, and refractive index. By the geometrical approach; we can find the angle of refraction. Once the angle of refraction is known; substitute it with the given value of angle of incidence, so that the refractive index can be determined.
Formula used:
\[\dfrac{\sin i}{\sin r}=\mu \]
\[\sin 2A=2\sin A\cos A\]

Complete step-by-step solution:

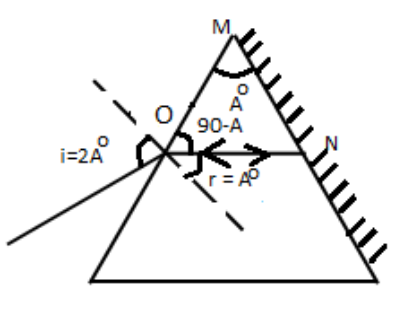
Given that,
The angle of prism \[=A\]
Angle of incidence, \[i=2A\]
From the above diagram,
\[\angle MON=90-A\]
Then,
\[\angle r=90-\left( 90-A \right)\]
\[\angle r=A{}^\circ \]
We have Snell’s law,
\[\dfrac{\sin i}{\sin r}=\mu \] ------- 1
Where,
\[i\] is the angle of incidence
\[r\]is the angle of refraction
\[\mu \]is the refractive index
Here,
\[i=2A{}^\circ \]
\[r=A{}^\circ \]
Then, substitute the values of \[i\]and \[r\]in equation 1. Then,
\[\dfrac{\sin 2A}{\sin A}=\mu \]
We have, \[\sin 2A=2\sin A\cos A\]
Then,
\[\dfrac{2\sin A\cos A}{\sin A}=\mu \]
\[\Rightarrow 2\cos A=\mu \]
Therefore, the refractive index of the prism, \[\mu =2\cos A\]

Additional information:
A prism is an optical element with polished flat surfaces, which refracts light. A traditional triangular prism has a triangular base with two rectangular sides. Prisms can be used to split light into its components. When light rays travel from one medium to the other, it gets refracted and enters the new medium at a different angle. The angle that the incident beam of light makes with the surface of the prism decides the degree of bending of the light's path. The ratio between the refractive indices of the two media is called Snell's law.

Note: Snell's law relates the angle of incidence and the angle of transmission to the refractive index of materials. While measuring the angles, it should be noted that the angles should be measured from the normal line drawn at the interface.
The unique shape of the prism makes the emergent rays bend at an angle, which is known as the angle of deviation. When white light is passed through the prism, it will split into seven colors because the angle of refraction is different for different colors. This phenomenon is called dispersion. And these colors can be combined to form white light using an inverted prism.