Question

The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.
a) 120,60,120,60
b) 110,70,110,70
c) 125,55,125,55
d) 115,65,115,65

Answer 1

Hint: Drop the altitudes on the 2 different sides of the parallelogram through one obtuse
vertex and after that apply angle sum property appropriately.

Complete step-by-step answer:

First draw a parallelogram ABCD.

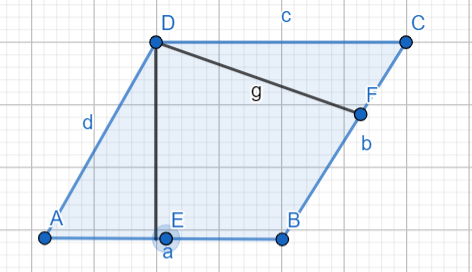
From vertex D drop perpendiculars on both the sides and they meet the sides on point E and F.
Now we have a parallelogram BEDF in which 2 angles are equal to 90 degrees.
Now we know that sum of all angles of a parallelogram is equal to 360 degrees.
So $\angle FBE$ = 360 – (90 +90 + 60).
$\angle FBE$= 360 – 240.
$\angle FBE$= 120 degrees.
In a parallelogram the opposite angles are same so that gives us two angles as 120.
Now sum of all the angles of a parallelogram is 360. So, for other 2 angles: -
2($\angle A$) = 360-(120 + 120).
2$\angle A$ = 360 – 240.
2$\angle A$= 120.
$\angle A$= 60.
Now Since opposite angles of a parallelogram are equal and adjacent angles of a parallelogram sum up to 180 degrees we can conclude all the angles of the parallelogram as 60,120,60,120
Hence, Option a is the correct answer.
Note: In this question, we do not need to find the rest of the angles of a parallelogram. After finding one angle we can spot the answer as all the options given in the question differ from each other.