Question

The age of Sarthak is one fifth the age of his mother and the sum of ages of Sarthak and his mom is equal to the age of Sarthak’s father. After 15 years the sum of ages of Sarthak and his mother will be four third the age of Sarthak’s father. The ratio of the present ages of Sarthak, mother and father respectively is:
[a] 1:5:7
[b] 2:10:10
[c] 1:5:6
[d] 2:8:9

Answer 1

- Hint: Assume the present age of Sarthak be x and the present age of his father be y. From the statement of the question form two linear equations in two variables x and y. Solve the system of equations using the substitution method or graphically or using matrices. Hence find the age of Sarthak, Sarthak’s mother and Sarthak’s father and hence find the ratio of their present ages.

Complete step-by-step solution -

Let the present age of Sarthak be x, and the age of his father be y. So the age of Sarthak’s mother is 5x.
Now according to the question, the sum of ages of Sarthak and his mother is equal to the age of Sarthak’s father.
So we have
5x+x=y
i.e. y = 6x (i)
Also after 15 years the sum of ages of Sarthak and his mother is $\dfrac{4}{3}$ times the age of his father.
Hence, we have
\[\begin{align}
  & x+15+5x+15=\dfrac{4}{3}y \\
 & \Rightarrow 6x+30=\dfrac{4}{3}y \\
 & \Rightarrow 18x+90=4y \\
 & \Rightarrow 9x-2y+45=0\ \ \ \ (\text{ii)} \\
\end{align}\]
Substituting the value of y from equation (i) in equation (ii), we get.
9x-2(6x)+45=0
i.e. -3x+45 = 0
Hence x = 15.
Substituting the value of equation (i), we get
y = 6(15) = 90.
Hence the age of Sarthak’s mother = 5x = 75.
Hence the ratio = 15:75:90 = 1:5:6

Note: We do not need to solve the system completely.
We know the age of Sarthak =x.
Age of Sarthak’s mother = 5x
And the age of Sarthak’s father = 6x
Hence the ratio = x:5x:6x = 1:5:6.
[2] We can also solve the system graphically.
Plotting the graphs of y = 6x and 9x-2y+45=0

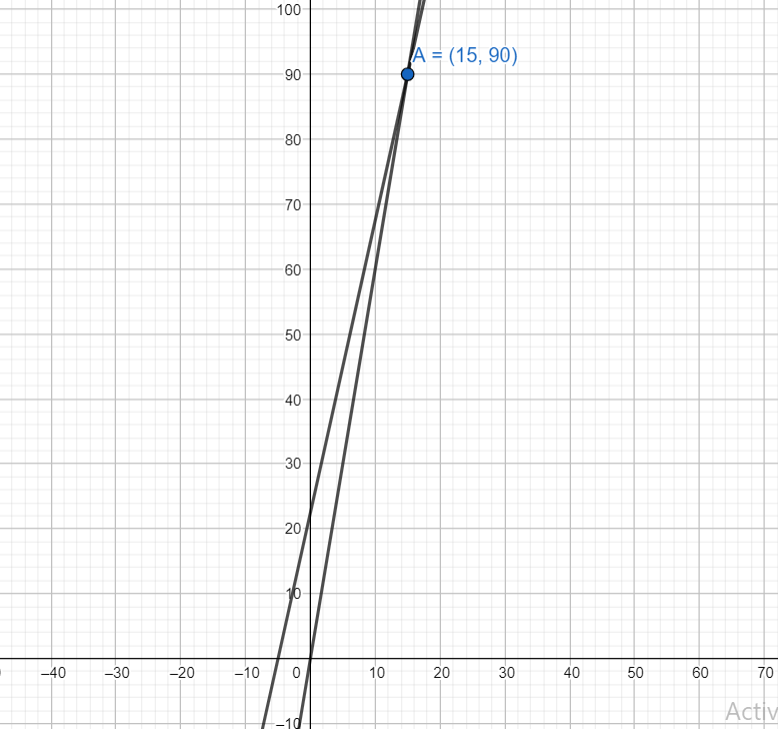
From the graph, it is clear that the lines intersect at x=15 and y = 90.