
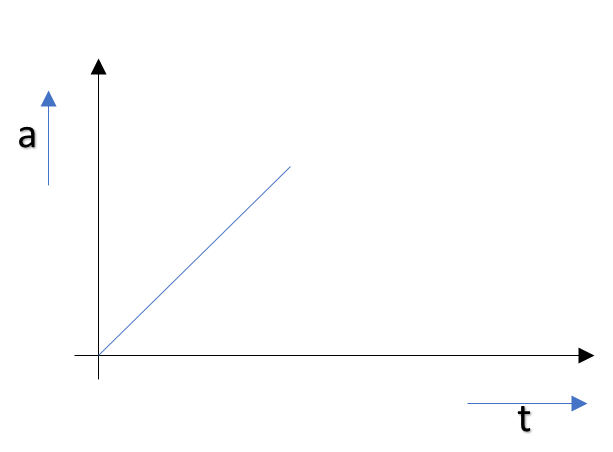
The acceleration-time graph of a body is shown in the figure. The most probable velocity-time graph of the body is:
A.)
B.)
C.)
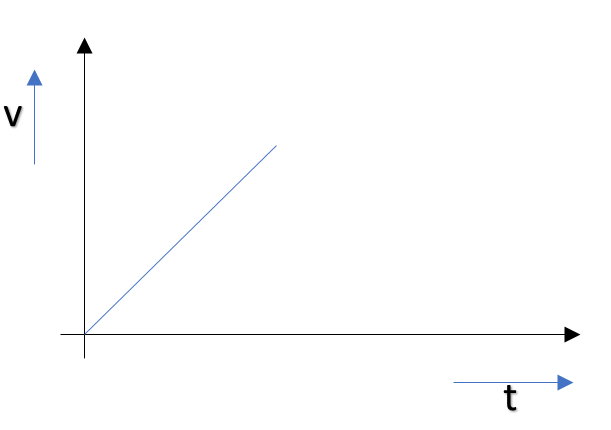
D.)





Answer
587.4k+ views
Hint: Considering only the motion of particles due to natural parameters like gravity, any motion on earth could be divided into two categories viz. straight line and parabolic path. A motion is parabolic if the initial velocity is not in the direction of acceleration due to gravity. Whereas a motion is a straight line only if either the velocity is zero or is in or opposite to the direction of acceleration due to gravity.
Formula used:
$a = \dfrac{dv}{dt}$
Complete answer:
Here, we are asked about the nature of the velocity time graph. Thus our foremost step must be to find the relation between velocity and time. Since the acceleration and time relation is linear, thus we can write:
$a = kt$, which is the equation of a line passing through the origin and having slope ‘m’.
Now, as acceleration is defined as the rate of change of velocity i.e. $a = \dfrac{dv}{dt}$, thus
$\dfrac{dv}{dt} = kt$
Or $dv = kt\ dt$
Integrating the equation without considering the constant of integration, we get;
$\int dv = \int ktdt = k\int tdt = k\dfrac{t^2}{2}$
Or $v= \dfrac{kt^2}{2}$.
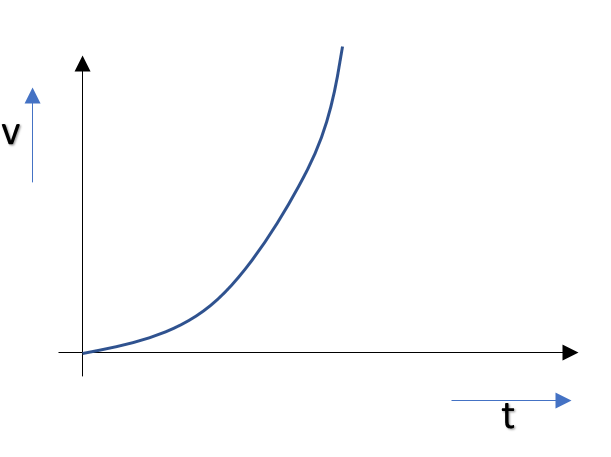
Hence, the relationship between velocity and time is parabolic. Thus the correct plot of velocity and time will be
So, the correct answer is “Option D”.
Note:
But saying that it moves in a parabolic path won’t be correct. For that we have to establish an equation between ‘x’ and ‘y’ coordinates. As it is not mentioned anywhere about the initial conditions of motion of the body, thus we can’t say anything about the actual motion of the particle. Also, we can observe here that the acceleration is not constant with time. Thus it can’t be the case of free fall motion.
Formula used:
$a = \dfrac{dv}{dt}$
Complete answer:
Here, we are asked about the nature of the velocity time graph. Thus our foremost step must be to find the relation between velocity and time. Since the acceleration and time relation is linear, thus we can write:
$a = kt$, which is the equation of a line passing through the origin and having slope ‘m’.
Now, as acceleration is defined as the rate of change of velocity i.e. $a = \dfrac{dv}{dt}$, thus
$\dfrac{dv}{dt} = kt$
Or $dv = kt\ dt$
Integrating the equation without considering the constant of integration, we get;
$\int dv = \int ktdt = k\int tdt = k\dfrac{t^2}{2}$
Or $v= \dfrac{kt^2}{2}$.
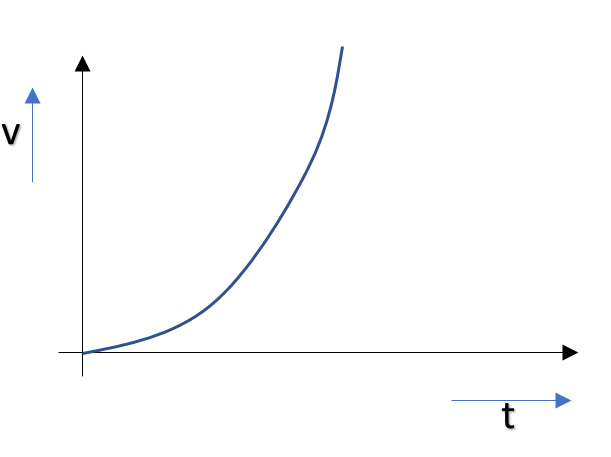
Hence, the relationship between velocity and time is parabolic. Thus the correct plot of velocity and time will be

So, the correct answer is “Option D”.
Note:
But saying that it moves in a parabolic path won’t be correct. For that we have to establish an equation between ‘x’ and ‘y’ coordinates. As it is not mentioned anywhere about the initial conditions of motion of the body, thus we can’t say anything about the actual motion of the particle. Also, we can observe here that the acceleration is not constant with time. Thus it can’t be the case of free fall motion.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Draw a diagram of nephron and explain its structur class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

Chemical formula of Bleaching powder is A Ca2OCl2 B class 11 chemistry CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

A solution of a substance X is used for white washing class 11 chemistry CBSE

Differentiate between calcination and roasting class 11 chemistry CBSE




