Question

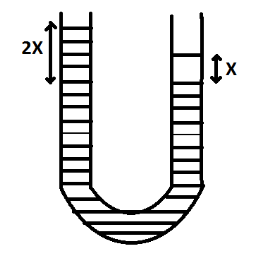
The $9kg$ solution is poured into a glass U-tube as shown in the figure below. The tube’s inner diameter is $2\sqrt {\dfrac{\pi }{5}} m$ and the solution oscillates freely up and down about its position of equilibrium$\left( {x = 0} \right)$. The period of oscillation in seconds is: ($1{m^3}$of solution has a mass $\mu = 900kg$, $g = 10m/{s^2}$. Ignore frictional and surface tension effects)

A. $0.1$
B. $10$
C. $\sqrt \pi $
D. $1$

Answer 1

Hint:Here, we are given a mass of a solution in the volume of $1{m^3}$which can be taken as the density of the material. We can equate the mass poured in the solution with the density multiplied by the volume of the liquid which is oscillating. By this we can find the oscillation length which is further used to find the period of oscillation.

Formulas used:
$V = \pi {r^2}l$,
where, $V$ is the volume, $r$ is the inner radius of tube and $l$ is the length of oscillation
$\rho = \dfrac{m}{V}$ ,
where, $\rho $ is the density of the liquid, m is the mass of liquid and $V$ is the volume of the liquid
$T = 2\pi \sqrt {\dfrac{l}{{2g}}} $,
Where, $T$ is the period of oscillation, $l$ is the length of oscillation and $g$ is the gravitational acceleration

Complete step by step answer:
We know that $h$
$
\rho = \dfrac{m}{V} \\
\Rightarrow m = \rho V \\ $
We will put $m = 9kg$, $\rho = 900kg/{m^3}$and $V = \pi {r^2}l$
$ \Rightarrow 9 = 900\pi {r^2}l$
We are given that $r = 2\sqrt {\dfrac{\pi }{5}} m$
$
9 = \dfrac{{900{\pi ^2}l}}{5} \\
\Rightarrow l = \dfrac{5}{{100{\pi ^2}}} $
Now, to find the period of oscillation we will use the formula:
$
T = 2\pi \sqrt {\dfrac{l}{{2g}}} \\
\Rightarrow T = 2\pi \sqrt {\dfrac{5}{{200{\pi ^2} \times 10}}} \\
\therefore T = 0.1s $

Thus, option A is the right answer.

Note:For solving this question, we have used the time period of oscillating fluid. Here we can clearly see that the time period of oscillating fluid is different from the time period of simple oscillation. To be precise, it is $\dfrac{1}{{\sqrt 2 }}$times the normal oscillation such as a simple pendulum.