Question

How do you tessellate a quadrilateral?

Answer 1

Hint: To tessellate a quadrilateral, we first of all need to understand what tessellation means. Tessellation means a pattern created by using identical shapes which fit together in such a way so that no gaps will be there. So, basically, we need to use identical quadrilateral shapes and fit them together in such a way so that no gaps will be there.

Complete step by step solution:
We know that a quadrilateral is a polygon with 4 sides. Though internal angles are different but the sum of these internal angles is ${{360}^{\circ }}$ so we can tessellate a quadrilateral.
Generally, these quadrilaterals cannot tile a plane but we can tile the quadrilateral by rotating the quadrilateral by ${{180}^{\circ }}$. In the below diagram, we have shown a quadrilateral which we are going to tile as follows:

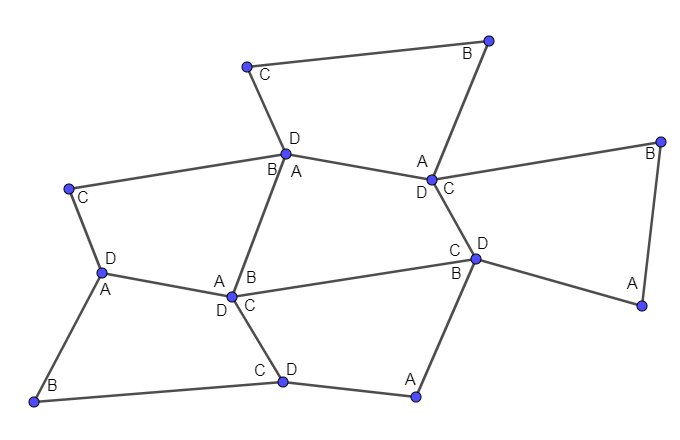
From the above figure, you can see that on the side of quadrilateral AD the quadrilateral which lies on the side AD is the same as the quadrilateral ABCD but it is rotated by ${{180}^{\circ }}$. You can see the rotation of ${{180}^{\circ }}$ as in place of vertex A we have D and in place of vertex D we have vertex A. Similarly, you can check this rotation of the quadrilateral on the remaining three sides (like BC, CD and AB). In this way, we have tessellated a quadrilateral.

Note: The mistake that could be possible in the above problem is that in the definition of tessellation, we have written the we use identical shapes to create a pattern so you might have forgot that we use identical shapes and forget to write this identical word in the definition of tessellation and further in drawing the quadrilateral so make sure you won’t make this mistake.