Question

Tension in the rope at the rigid support is $\left( g=10m/{{s}^{2}} \right)$

$A)\text{ }760N$
$B)\text{ 13}60N$
$C)\text{ 158}0N$
$D)\text{ 1}620N$

Answer 1

Hint: This problem can be solved by drawing the proper free body diagrams for each of the three men and writing the force equations in the form of Newton’s second law of motion which states that the net force exerted on a body is the product of its mass and the acceleration of the body produced due to that force. The tension in the rope due to each man will be different and the total tension in the rope will be the sum of these different individual tensions.
Formula used:
$F=ma$
$W=mg$

Complete step by step answer:
We can solve this problem by finding out the individual tensions in the rope due to the actions of the three men. The total tension at the rigid support will be the sum of these three individual tensions. To do so, we will draw proper free body diagrams and apply the force-acceleration equation for each man.
The magnitude of net force $F$ on a body of mass $m$and having acceleration $a$ in the direction of the applied force is given by
$F=ma$ --(1)
Hence, let us proceed to do that.
Weight $W$ of a body of mass $m$ is given by
$W=mg$ --(2)
where $g$ is the acceleration due to gravity.

Throughout the problem, we will consider accelerations and forces in the upward direction (from the free end of the rope towards the rigid support) to be positive and in the downward direction to be negative.
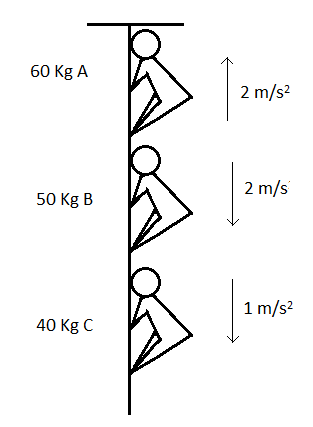
Let the mass of man A be ${{M}_{A}}=60kg$.
The acceleration of man A is ${{a}_{A}}=2m/{{s}^{2}}$.
The tension in the rope due to the actions of man A be ${{T}_{A}}$. The rope exerts this tension on the man in the upward direction.
Let the weight of man A be ${{W}_{A}}$. Using (2), we get,
${{W}_{A}}=60g$. --(3)
Let us draw the free body diagram of man A. There are two forces on him, the upward tension due to the rope and his weight downward.
 

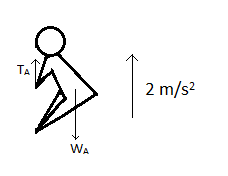
Therefore, using (1), we get,
${{T}_{A}}-{{W}_{A}}={{M}_{A}}{{a}_{A}}$
$\therefore {{T}_{A}}-60g=60\times 2=120$ [Using (3)]
$\therefore {{T}_{A}}=120+60g=120+\left( 60\times 10 \right)=120+600=720N$ $\left( \because g=10m/{{s}^{2}} \right)$
$\therefore {{T}_{A}}=720N$ --(4)

Let the mass of man B be ${{M}_{B}}=50kg$.
The acceleration of man B is ${{a}_{B}}=0$. (Since, the man is moving down with constant velocity equal to $2m/s$, he has zero acceleration)
The tension in the rope due to the actions of man B be ${{T}_{B}}$. The rope exerts this tension on the man in the upward direction.
Let the weight of man B be ${{W}_{B}}$. Using (2), we get,
${{W}_{B}}=50g$. --(5)
Let us draw the free body diagram of man B. There are two forces on him, the upward tension due to the rope and his weight downward.
 

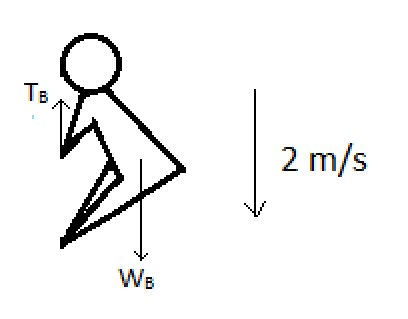
Therefore, using (1), we get,
${{T}_{B}}-{{W}_{B}}={{M}_{B}}{{a}_{B}}$
$\therefore {{T}_{B}}-50g=50\times 0=0$ [Using (5)]
$\therefore {{T}_{B}}=50g=\left( 50\times 10 \right)=500N$ $\left( \because g=10m/{{s}^{2}} \right)$
$\therefore {{T}_{B}}=500N$ --(6)

Let the mass of man C be ${{M}_{C}}=40kg$.
The acceleration of man C is ${{a}_{C}}=-1m/{{s}^{2}}$.
The tension in the rope due to the actions of man C be ${{T}_{C}}$. The rope exerts this tension on the man in the upward direction.
Let the weight of man C be ${{W}_{C}}$. Using (2), we get,
${{W}_{C}}=40g$. --(7)
Let us draw the free body diagram of man C. There are two forces on him, the upward tension due to the rope and his weight downward.
 

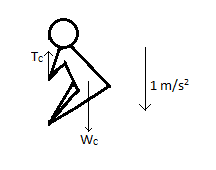
Therefore, using (1), we get,
${{T}_{C}}-{{W}_{C}}={{M}_{C}}{{a}_{C}}$
$\therefore {{T}_{C}}-40g=40\times \left( -1 \right)=-40$ [Using (7)]
$\therefore {{T}_{C}}=-40+40g=-40+\left( 40\times 10 \right)=-40+400=360N$ $\left( \because g=10m/{{s}^{2}} \right)$
$\therefore {{T}_{C}}=360N$ --(8)
The total tension in the rigid support has to balance the tensions in the rope due to individual actions of the three men.
Let the total tension at the rigid support be $T$.
$\therefore T={{T}_{A}}+{{T}_{B}}+{{T}_{C}}$
Therefore, using (4), (6) and (8), we get,
$T=720+500+360=1580N$
Hence, the total tension at the rigid support is $1580N$.
Hence, the correct option is $C)\text{ 158}0N$.

Note: Students might think that the rope has a constant tension throughout its length and proceed to calculate the tension by taking it constant for all the three men in the force-acceleration equations. However, this is not true and will lead to an erroneous result. The tension in the rope due to the actions of the three men is different and is seen in the part of the rope above the place where they hold it. For example if a single person hangs from a rope, the part of the rope below the point where he holds it, remains loose and can dangle which means there is no tension in it and the tension in the rope is not constant throughout the length. Hence, students can make this error in this question if they do not understand this concept properly.