Question

How can I tell whether a parabola opens upward or downward?

Answer 1

Hint: In order to know whether which side parabola is facing, we have to see its highest order term that is the coefficient of the ${{x}^{2}}$ term. If we want to see it graphically, it will look like a bowl instead of a mountain.

Complete step by step solution:
A quadratic function is a second degree polynomial function. The general form of a quadratic function is this: \[f~\left( x \right)\text{ }=~a{{x}^{2}}~+~bx~+~c,\] where \[a,~b,\] and \[c\] are real numbers, and \[a\ne \text{ }0.\]
The graph of a quadratic function is called a parabola.
A parabola is roughly shaped like the letter ‘U’ or upside-down ‘U’.
There is an easy way to tell whether the graph of a quadratic function opens upward or downward:
If the leading coefficient is greater than zero, the parabola opens upward, and if the leading coefficient is less than zero, the parabola opens downward.
We can illustrate with the help of following graphs:

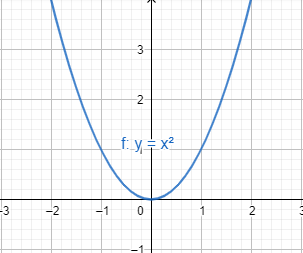
The function above, \[y~=~{{x}^{2}}\], has leading coefficient \[a~=1\ge 0\], so the parabola opens upward.

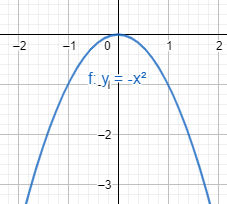
Also, the other function above, has leading coefficient $-1$, so the parabola opens downward.
The standard form of a quadratic function is a little different from the general form.
The standard form of the equation makes it easier to graph.
The standard form of equation is as follows: 
\[f~\left( x \right)\text{ }=~a{{\left( x~-~h \right)}^{2}}~+~k,\] where \[a\ne 0\].
In standard form, \[h=-\dfrac{b}{2a}\] and $k=c-\dfrac{{{b}^{2}}}{4a}$.
The point \[\left( h,~k \right)\] is called the vertex of the parabola.
The line \[x~=~h\] is called the axis of the parabola.
A parabola is symmetrical with respect to its axis.
The value of the function at \[h~=~k.\]
If \[a~<0\], then $k$ is the maximum value of the function.
If \[a~>0\], then $k$ is the minimum value of the function.
That is, if \[x~>0\], then we can tell parabola is facing upward and if \[x~<0\] then we can tell parabola is facing downward.

Note: There will always be a problem while using any quadratic formula, therefore the term that will provide us the overall direction to the equation will be the leading term, or the term with the highest power.
If the term is positive, then as ${{x}^{2}}$ dominates the $x$ term with bigger values of $\left| x \right|$.
The result of the equation will become bigger and bigger.