Question

Tangents are drawn to the circle \[{{x}^{2}}+{{y}^{2}}=9\] at the points where it is met by the circle \[{{x}^{2}}+{{y}^{2}}+3x+4y+2=0\] . Find the point of intersection of these tangents.

Answer 1

Hint: The equation of the circles are \[{{S}_{1}}={{x}^{2}}+{{y}^{2}}-9=0\] and \[{{S}_{2}}={{x}^{2}}+{{y}^{2}}+3x+4y+2=0\] . Use the formula for the common chord for the circle whose equation is represented by \[{{S}_{1}}=0\] and \[{{S}_{2}}=0\] , \[{{S}_{1}}-{{S}_{2}}=0\] and get the equation for the common chord AB. We also know the formula for the chord of contact for point \[\left( {{x}_{1}},{{y}_{1}} \right)\] of circle \[{{x}^{2}}+{{y}^{2}}-{{a}^{2}}=0\] , \[x{{x}_{1}}+y{{y}_{1}}-{{a}^{2}}=0\] . Now, get the equation for the chord of contact and then compare it with the equation of common chord to get the value of \[{{x}_{1}}\] and \[{{y}_{1}}\] .

Complete step by step answer:
According to the question, we are given that
The equation of the first circle is \[{{S}_{1}}={{x}^{2}}+{{y}^{2}}-9=0\] ………………………………….(1)
The equation of the second circle is \[{{S}_{2}}={{x}^{2}}+{{y}^{2}}+3x+4y+2=0\] ………………………………………….(2)
Now, let us draw the diagram for both circles using equation (1) and equation (2).

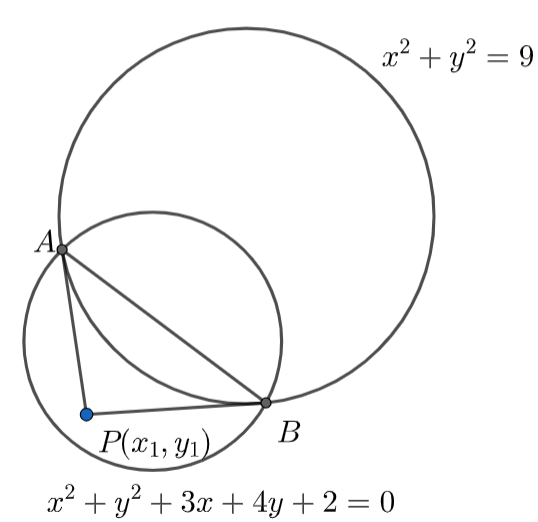
In the above diagram, we can observe that AB is the common chord for the circle \[{{S}_{1}}\] and \[{{S}_{2}}\].
We know the formula for the common chord for the circle whose equation is represented by \[{{S}_{1}}=0\] and \[{{S}_{2}}=0\] , \[{{S}_{1}}-{{S}_{2}}=0\] ………………………………………….(3)
Now, from equation (1), equation (2), equation (3), we get
\[\begin{align}
  & \Rightarrow {{S}_{1}}-{{S}_{2}}=0 \\
 & \Rightarrow \left( {{x}^{2}}+{{y}^{2}}-9 \right)-\left( {{x}^{2}}+{{y}^{2}}+3x+4y+2 \right)=0 \\
 & \Rightarrow -9-3x-4y-2=0 \\
\end{align}\]
\[\Rightarrow 3x+4y+11=0\] ……………………………………(4)
Since PA and PB are tangents for the circle \[{{S}_{1}}={{x}^{2}}+{{y}^{2}}-9=0\] which is meeting at point P so, from the above diagram we can also say that AB is the chord of contact for the circle \[{{S}_{1}}={{x}^{2}}+{{y}^{2}}-9=0\] …………………………………….(5)
We also know the formula for the chord of contact for point \[\left( {{x}_{1}},{{y}_{1}} \right)\] of circle \[{{x}^{2}}+{{y}^{2}}-{{a}^{2}}=0\] , \[x{{x}_{1}}+y{{y}_{1}}-{{a}^{2}}=0\] ………………………………………(6)
Now, from equation (5) and equation (6), we get
The equation of the chord of contact AB = \[x{{x}_{1}}+y{{y}_{1}}-9=0\] …………………………………….(7)
But from equation (4), we have the equation of the chord of contact AB ……………………………………..(8)
Equation (4) and equation (7) represents the same line AB. So, their coefficients must be proportional ……………………………………(9)
Now, from equation (4), equation (7), equation (8), and equation (9), we get
\[\dfrac{{{x}_{1}}}{3}=\dfrac{{{y}_{1}}}{4}=\dfrac{-9}{11}\] ……………………………………(10)
On solving equation (10), we get
\[{{x}_{1}}=\dfrac{-27}{11}\] , \[{{y}_{1}}=\dfrac{-36}{11}\] .
Therefore the coordinate of the point of the intersection of tangents drawn to the circle \[{{x}^{2}}+{{y}^{2}}=9\] at the points where it is met by the circle \[{{x}^{2}}+{{y}^{2}}+3x+4y+2=0\] is \[\left( \dfrac{-27}{11},\dfrac{-36}{11} \right)\] .

Note:
For this type of question, we have to consider two points. The first one is the equation of the common chord for the circle whose equations are represented by \[{{S}_{1}}=0\] and \[{{S}_{2}}=0\] is \[{{S}_{1}}-{{S}_{2}}=0\] . The equation of the chord of contact for point \[\left( {{x}_{1}},{{y}_{1}} \right)\] of the circle \[{{x}^{2}}+{{y}^{2}}-{{a}^{2}}=0\] is \[x{{x}_{1}}+y{{y}_{1}}-{{a}^{2}}=0\] .