Question

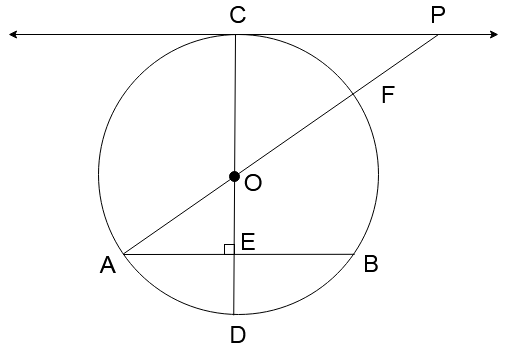
Tangent \[\overleftrightarrow {PC}\] intersects the circle \[O\] at \[C\] , chord \[\overline {AB} ||\overleftrightarrow {CP}\] , diameter \[\overline {COD} \] intersects \[\overline {AB} \] at \[E\] , and diameter \[\overline {AOF} \] is extended to \[P\] . If \[m\angle OAE = 30\] , find \[m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{AD} \] , \[m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{CF} \] .

Answer 1

Hint: You can start by explaining why we need to calculate the angles corresponding to the given arcs and write the equation for finding the length of the arc, i.e. Length of an arc \[ = 2\pi r\dfrac{n}{{360}}\] . Then calculate the angle \[\angle AOE\] by using the property of the triangle that states that the sum of all the angles in a triangle is \[180^\circ \] . Then use the concept of vertically opposite angles to find \[\angle COF\] . Then put these values in the equation Length of an arc \[ = 2\pi r\dfrac{n}{{360}}\] to reach the solution.

Complete step by step answer:
Now, in this problem, we have to find \[m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{AD} \] and \[m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{CF} \] . Both of these are arcs and we know for a fact that the length of an arc can be calculated by using the angle which the two ends points of the arc make at the center. For this, we use the following equation
Length of an arc \[ = 2\pi r\dfrac{n}{{360}}\] (Equation 1)
Here, \[n = \] the angle that the two endpoints of the arc make at the center
So in this case to calculate \[m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{AD} \] we have to calculate \[\angle AOE\] and to find out \[m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{CF} \] , we have to calculate the value of \[\angle COF\] .
To solve this question we will first use a very interesting property of triangles. A triangle has 3 angles and the sum of all the three angles is always equal to \[180^\circ \] .
So, we now know that in $\Delta AOE$
$\angle AOE + \angle OEA + \angle OAE = 180^\circ $
Given in the problem,
\[\angle OAE = 30^\circ \]
\[\angle OEA = 90^\circ \] (Chords are always perpendicular to the radius)
So, \[\angle AOE + 90^\circ + 30^\circ = 180^\circ \]
\[\angle AOE = 60^\circ \]
We can also say that
\[\angle AOE = \angle COF = 60^\circ \] (Vertically opposite angles)
Now using equation 1 to calculate the value of \[m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{AD} \] , we get
\[m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{AD} = 2\pi r\dfrac{{60}}{{360}}\]
\[m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{AD} = \dfrac{1}{3}\pi r\]
Now using equation 1 to calculate the value of \[m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{CF} \] , we get
\[m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{CF} = 2\pi r\dfrac{{60}}{{360}}\]
\[m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{CF} = \dfrac{1}{3}\pi r\]
Hence, \[m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{AD} \] and \[m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{CF} \] are both equal to \[\dfrac{1}{3}\pi r\] .

Note: In such a type of problem we can easily solve it by using the basic properties of arcs in a circle. But, it is especially very important to remember what symbols represent what part. For example, we are given \[\overleftrightarrow {PC}\] that represents a tangent, \[\overline {COD} \] that represents a diameter, \[\overline {AB} \] represents a chord, and \[m\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{AD} \] represents an arc.