Question

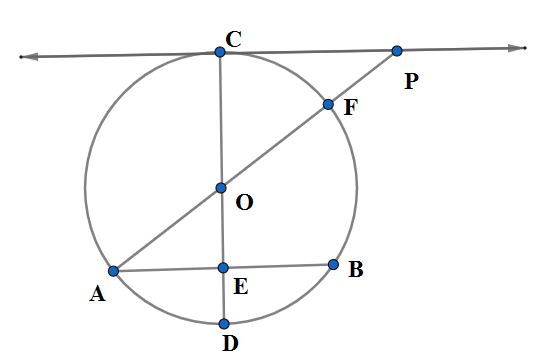
Tangent $\overleftrightarrow {PC}$. intersects circle with centre $O$ at $C$, chord $\overline {AB} ||\overleftrightarrow {CP}$ ,diameter $\overline {COD} $ intersects AB at $E$ and diameter $\overline {AOF} $ is extended to $P.$
If $m\angle OAE = {30^ \circ }$ find $m\widehat {AC}$ and $m\angle P$. \[\]

Answer 1

Hint: We use the equality of measures of alternate angles subtended by the transverse AP to have $m\angle OAE = m\angle OPC = m\angle P$. We use the theorem that radius and tangent are perpendicular to have$\angle OCP = {90^ \circ }$. We find the arc measure $m\widehat {AC} = m\angle AOC = {180^ \circ } - m\angle COP$.\[\]

Complete step-by-step solution:
We are given in the question that tangent $\overleftrightarrow {PC}$ intersects circle with centre $O$ at $C$, chord $\overline {AB} ||\overleftrightarrow {PC}$ ,diameter $\overline {COD} $ intersects AB at $E$ and diameter $\overline {AOF} $ is extended to $P.$We know that tangent and radius of circle are always perpendicular to each other. So here the tangent $\overleftrightarrow {PC}$ is perpendicular to radius OC. Hence we have
\[m\angle OCP = {90^ \circ }\]
 We know that when a transversal intersects two parallel lines the measure of alternate angles are equal. Here we are given the parallel lines $\overline {AB} ||\overleftrightarrow {CP}$. We observe the transverse AP which subtends alternate angles $\angle OPC,\angle OAE$. We are given in the question that $m\angle OAE = {30^ \circ }$.So by equality of alternate angles we have;
\[m\angle OPC = m\angle OAE = {30^ \circ }\]
We know that the sum of measures of internal angles is ${180^ \circ }$. The internal angles of triangle OPC are$\angle OPC,\angle OCP,\angle COP$.So we have
\[m\angle OPC + m\angle OCP + m\angle OCP = {180^ \circ }\]
We put previously obtained $m\angle OPC = {30^ \circ },m\angle OCP = {90^ \circ }$ in above equation to have
\[\begin{gathered}
  m\angle OPC + m\angle OCP + m\angle COP = {180^ \circ } \\
   \Rightarrow {30^ \circ } + {90^ \circ } + m\angle COP = {180^ \circ } \\
   \Rightarrow m\angle COP = {180^ \circ } - {120^ \circ } = {60^ \circ } \\
\end{gathered} \]
We know that the sum of measured linear pairs of angles subtended on a straight line is ${180^ \circ }$. We see in the figure that the angles $\angle COA,\angle COP$ are linear pair of angles and hence
\[\begin{gathered}
  m\angle COA + m\angle COP = {180^ \circ } \\
   \Rightarrow m\angle COA + {60^ \circ } = {180^ \circ } \\
   \Rightarrow m\angle COA = {180^ \circ } - {60^ \circ } = {120^ \circ } \\
\end{gathered} \]
So we have
\[m\widehat {AC} = m\angle COA = {120^ \circ }\]
So the required results are $m\widehat {AC} = {120^ \circ },m\angle P = {30^ \circ }$.\[\]

Note: We note that the angle measure of an arc is the angle the endpoints of the arc subtended at the centre (also called central angle). That is why $m\widehat {AC} = m\angle COA$.W can further prove that the triangles OAE and OPC are similar either by equality of alternate angles by the transverse CD to have $m\angle OEA = \angle OCP = {90^ \circ }$ or equality of vertically opposite angles $\angle COP = \angle AOE$ with angle-angle criterion.