Question

Tangent ABC intersects circle O to B. Secant AFOD intersects the circle at F and D, and secant CGOE intersects the circle at G and E. If \[m\overset\frown{EFB}=m\overset\frown{DGB}\], prove that \[\Delta AOC\] is isosceles.

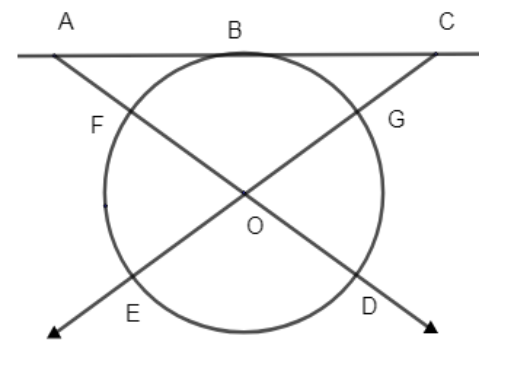
Answer 1

Hint: Join OB and use the property of tangent to a circle which says that “radius is perpendicular to the tangent at the point of contact”. Here, O is assumed as the center. Now, show that \[\angle AOB=\angle COB\], by first showing that, \[\angle EOF=\angle DOG\] using the rule of vertically opposite angles are equal. Finally, use A – S – A congruency criteria to prove \[\Delta AOB\] congruent to \[\Delta COB\] and hence, show that, AO = CO.

Complete step-by-step solution
Let us join OB where O is the center of the circle. So, the resultant figure will look like.

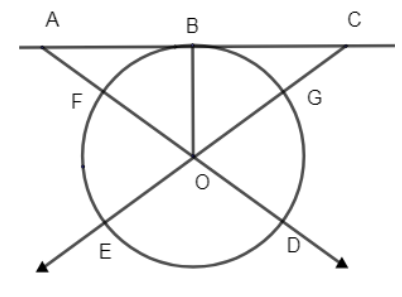
Now, we have to prove that AOC is an isosceles triangle. That means we have to prove, AO = CO.
We have been given that, \[m\overset\frown{EFB}=m\overset\frown{DGB}\], that means measure of arcs EFB and DGB are equal. We know that, equal angles at the center. Therefore,
\[\Rightarrow \angle EOB=\angle DOB\]
Now, \[\angle EOF=\angle DOG\] as they are vertically opposite angles and we know that such angles are equal.
\[\Rightarrow \angle EOB-\angle EOF=\angle DOG-\angle DOB\]
\[\Rightarrow \angle AOB=\angle COB\] - (i)
Let us consider \[\Delta AOB\] and \[\Delta COB\],
\[\Rightarrow \angle ABO=\angle CBO={{90}^{\circ }}\], since \[OB\bot ABC\].
\[\Rightarrow OB=OB\], common side in both triangles
\[\Rightarrow \angle AOB=\angle COB\], using relation (i)
\[\therefore \] We see that two angles and the included side of \[\Delta AOB\] are equal to the two angles and the included side of \[\Delta COB\]. Hence, \[\Delta AOB\] is congruent to \[\Delta COB\]. So, their corresponding sides must be equal.
\[\Rightarrow AO=CO\]
Now, in triangle AOC, we have proved that AO = CO.
Therefore, \[\Delta AOC\] is an isosceles triangle.

Note: One may note that in the above solution we have proved that the \[\Delta AOC\] is isosceles by proving that AO = CO. You may also prove \[\angle OAB=\angle OCB\] for the same. But first, we have to show that both the triangles are congruent which we did above using A – S – A congruency criteria. Here, the property of tangent and equal arcs are important things to remember.