Question

Take any point O in the interior of \[\vartriangle PQR\]. Is

(i) \[OP + OQ > PQ\]
(ii) \[OQ + OR > QR\]
(iii) \[OR + OP > RP\]

Answer 1

Hint:We join the three vertices to the interior point O. Taking each triangle formed inside the triangle PQR separately, we apply the rule that the sum of any two sides of a triangle is always greater than the third side of the triangle.

Complete step-by-step answer:
We join the vertices of triangle PQR with the point O that lies inside the triangle.

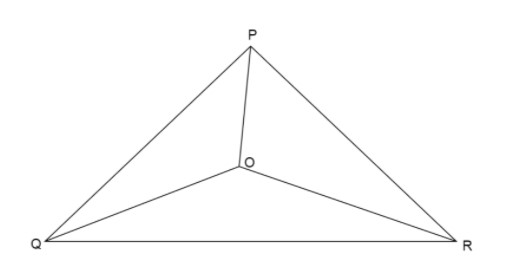
Now we take each triangle formed inside the triangle one by one.
(i)
Firstly, in \[\vartriangle OPQ\]
The three sides of the triangle are OP, OQ and PQ
Since we know the sum of any two sides of a triangle is greater than the third side.
Therefore, we can write \[OP + OQ > PQ\]
This proves our first part.
(ii)
Firstly, in \[\vartriangle OQR\]
The three sides of the triangle are OR, OQ and QR
Since we know the sum of any two sides of a triangle is greater than the third side.
Therefore, we can write \[OQ + OR > QR\]
This proves our second part.
(i)
Firstly, in \[\vartriangle OPR\]
The three sides of the triangle are OP, PR and OR
Since we know the sum of any two sides of a triangle is greater than the third side.
Therefore, we can write \[OR + OP > RP\]
This proves our third part.

So, the correct answer is “Option A”.

Note:Students can take any two pairs of sides as sum because the law holds for all the pairs of sides. But we don’t need to show all set of sides, we should only focus on the given options. We use > greater than sign where on the LHS of the sign > we write the value that is greater and on the RHS we write the value from which the LHS is greater.